实际问题与一元二次方程(第课时)VIP免费

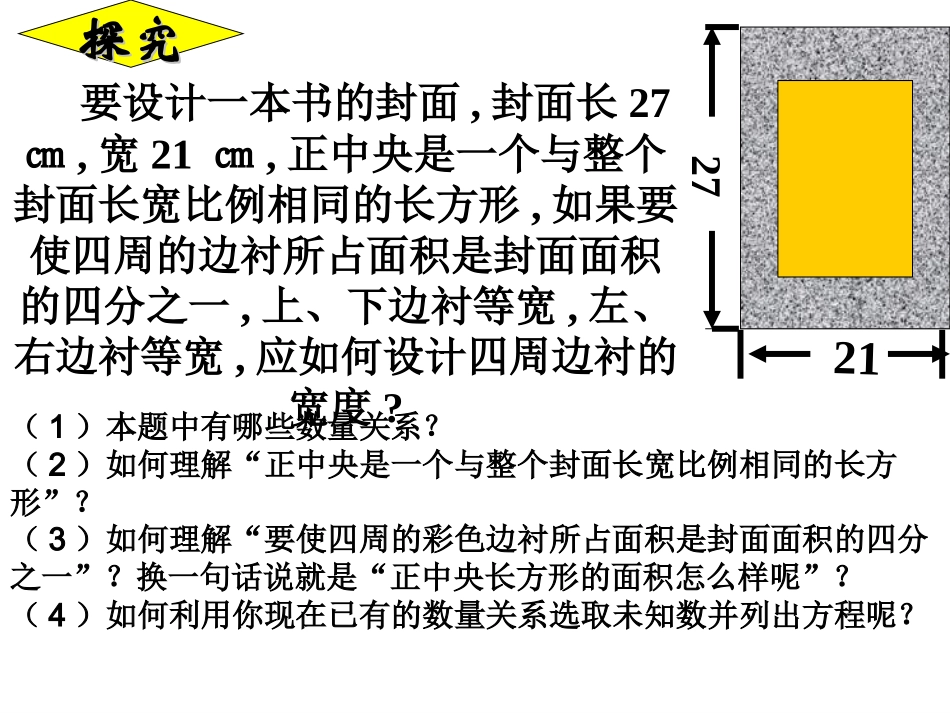
第二十二章一元二次方程第第33课时课时湖北省仙桃市第三中学刘烈武22.322.3实际问题与一元实际问题与一元二次方程二次方程复习：列方程解应用题有哪些步骤？①审题，②设未知数，③找出应用题中数量间的相等关系，④列出方程，⑤解方程，⑥检验并写出答案．要设计一本书的封面,封面长27㎝,宽21㎝,正中央是一个与整个封面长宽比例相同的长方形,如果要使四周的边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度?2721探究探究（1）本题中有哪些数量关系？（2）如何理解“正中央是一个与整个封面长宽比例相同的长方形”？（3）如何理解“要使四周的彩色边衬所占面积是封面面积的四分之一”？换一句话说就是“正中央长方形的面积怎么样呢”？（4）如何利用你现在已有的数量关系选取未知数并列出方程呢？2721分析:这本书的长宽之比是9:7,依题知正中央的矩形两边之比也为9:7.解法一:设正中央的矩形两边分别为9xcm，7xcm，依题意得.21274379xx解得,2331x).,(2332舍去不合题意x故上、下边衬的宽度为:左、右边衬的宽度为:.8.143275422339272927x.4.143214222337212721x要设计一本书的封面,封面长27㎝,宽21㎝,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度?2721同学们讨论一下本题还有其他的方法吗？（1）“正中央是一个与整个封面长宽比例相同的长方形”是否说明上、下边衬与左、右边衬都等宽？（2）如若不等宽，那么上、下边衬与左、右边衬之间是否有一个比例关系呢，是多少？（3）你能否利用这种比例关系，联系前面的数量关系，选取未知数并列出方程呢？2721分析:这本书的长宽之比是9:7,正中央的矩形两边之比也为9:7,由此判断上下边衬与左右边衬的宽度之比也为9:7.解法二:设上下边衬的宽为9xcm，左右边衬宽为7xcm，依题意得：.212743)1421)(1827(xx解方程得.4336x(以下同学们自己完成)方程的哪个根合乎实际意义?为什么?反思一下这两种解法的等量关系相同吗？它们的不同在哪里？例2某校为了美化校园,准备在一块长32米,宽20米的长方形场地上修筑若干条等宽的道路,余下部分作草坪,并请全校同学参与设计,现在有两位学生各设计了一种方案(如图),根据两种设计方案各列出方程,求图中道路的宽分别是多少时可使图(1),(2)的草坪面积为540米2？(1)(2)(1)解:(1)如图，设道路的宽为x米，则540)220)(232(xx化简得，025262xx0)1)(25(xx1,2521xx其中的x=25超出了原矩形的宽，应舍去.∴图(1)中道路的宽为1米.则横向的路面面积为，分析：此题的相等关系是矩形面积减去道路面积等于540米2.解法一：如图，设道路的宽为x米，32x米2纵向的路面面积为.20x米2注意：这两个面积的重叠部分是x2米2所列的方程是不是3220(3220)540xx？图中的道路面积不是3220xx米2.(2)而是从其中减去重叠部分，即应是23220xxx米2.所以正确的方程是：232203220540xxx化简得，2521000,xx其中的x=50超出了原矩形的长和宽，应舍去.取x=2时，道路总面积为：23222022=100(米2)草坪面积=3220100=540（米2）答：所求道路的宽为2米.122,50xx解法二：我们可不可以利用“图形经过移动，它的面积大小不会改变”的道理，把纵、横两条路移动一下，使列方程容易些（目的是求出路面的宽，至于实际施工，仍可按原图的位置修路）？(2)(2)解法二：如图，设路宽为x米，草坪矩形的长（横向）为，草坪矩形的宽（纵向）.相等关系是：草坪长×草坪宽=540米2(20-x)米（32-x)米即3220540.xx化简得：212521000,50,2xxxx再往下的计算、格式书写与解法1相同.课堂练习课堂练习见教科书P48习题22.3第8题.•这里要特别注意:在列一元二次方程解应用题时，由于所得的根一般有两个，所以要检验这两个根是否符合实际问题的要求．•列一元二次方程解应用题的步骤即审、设、找、列、解、检．小结：通过本节课的学习，大家有什么新的收获和体会？...