可化为一元一次方程的分式方程设计VIP免费

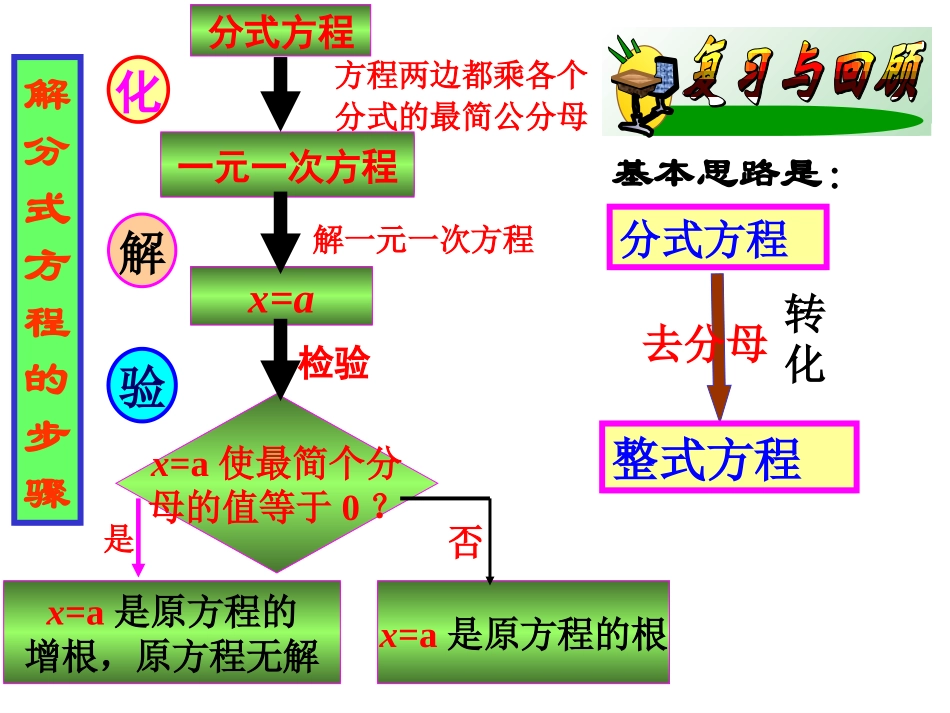
本节内容1.5(二)分式方程一元一次方程x=ax=a使最简个分母的值等于0？x=a是原方程的增根，原方程无解x=a是原方程的根否是方程两边都乘各个分式的最简公分母解一元一次方程检验解分式方程的步骤基本思路是：化解验分式方程去分母整式方程转化2、把分式方程化为一元一次方程是。x2+x+3x=13、方程的解是。x-323x-2=5、当x=时，分式的值与分式的值相等？4-x4-2xx-4x-51、判断下列式子哪些是分式方程？x+y=55x+2=32y-zx1x+5y=0x1+2x=54、如果x=2是分式方程的解，那么a=。ax-1x-3=-26、若方程有增根，则增根一定是。x+3mx+31+1=7、解方程(1).x90x-660=(2).x5x-27=(3).x-32x3=(4).x-11x2-12=×××√√x=6x=543-1x=-3x=18x=-5x=9无解举例例1解方程：7+3=.11xxx--解方程两边同乘最简公分母x-1，得7+3(x-1)=x.解这个一元一次方程，得x=-2.检验：把x=-2时，最简公分母x-1的值为:-2-1=-3≠0因此x=-2是原方程的一个根.例2解方程：x-1x+1-x2-14=1解方程两边同乘最简公分母x2-1，得：(x+1)2-4=x2-1解得：x=1检验：当x=1时，x-1=0,x2-1=0因此，x=1是增根，原方程无解。注意：分式方程化整式方程时，不含分母的项也要乘以最简公分母。1、判断下列解法是否正确：(1).解方程：去分母得：36(x-1)=30x+1x36=x-130+1(2).解方程：去分母得：3-2x2=(2x-4)-2x2-4x2x-43-2x2=-x31312、解方程(1).x-1x-1=(x-1)(x+2)336(x-1)=30x+x(x-1)3(3-2x2)=(2x-4)-3x(2x-4)x=1(增根)原方程无解13321xxxx（2）23x=-例1、解方程x-413x-310x-54x-11--=解解：：原方程变形为：(x-4)(x-3)3x+1(x-5)(x-1)3x+1=两边分别通分(1)若3x+1=0,即x=-时，原方程显然成立。31(2)若3x+1≠0，原方程的两边同除以3x+1得：(x-4)(x-3)1(x-5)(x-1)1=即：(x-4)(x-3)=(x-5)(x-1)解得：x=7经检验，x=-，x=7都是原方程的解。31分类讨论写出所有解例例22、、aa为何值时，解关于为何值时，解关于xx的方的方程：程：x-12x+2a+1x2+x-23a-=会产生增根？(a-1)x=5-2a当增根为x=1时，得：a=2当增根为x=-2时，a无解(不存在).故a=2时,原方程会产生增根.____axxaxx，则的增根是、方程111111.____mxmmx有增根，则的方程、若关于13122211(产生增根的原因)。(x=1,x=-2)分析：原方程产生的增根是多少？能否将这两个值直接代入原方程?因而先将分式方程化成整式方程.再把增根代入计算出a。1、解方程作业13321xxxx(1)524;2332xxx21424563524xxxx2283224xxxxx2、x为何值时，分式的值比分式的值大1？2-x3x-2x-3253242mxxx当m取何值时，关于x的方程=+有增根？3、中考试题2、分式方程的解是（）A.-3B.2C.3D.-253=2-xxA65563223;B.;C.;D.A.BB125xxxx与4.当x=()时,互为相反数.3、解分式方程，可知方程（）A.解为x=2B.解为x=4C.解为x=3D.无解11+2=22xxx---D1、分式方程的解为.12=+11-xxx=-3课外练习课外练习3221)1(xx1、解方程：2121)2(xxx015)3(22xxxx3、如果有增根，那么增根为.xxx21321x=22、关于x的方程=4的解是x=,则a=.xax12124、若分式方程有增根,则a=.04422xxa-15、若方程会产生增根，则（）A、k=±2B、k=2C、k=-2D、k为任何实数4xx412xk2x126、若关于x的方程，有增根，求a的值。13xax4x2Ba=37、解分式方程76122xx（1）01522xxxx(4).16235222xxxxx)5)(4(1)3)(2(18xxxx111.32xxxx212122339xxx22231xxx(6).221122xxx(7).