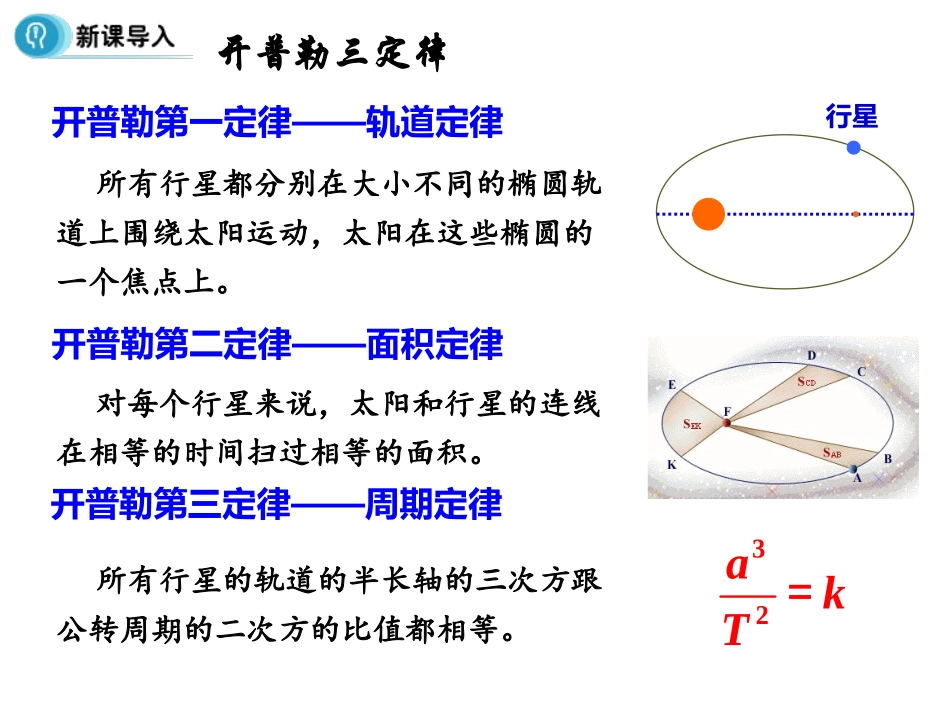
第2节:太阳与行星间的引力开普勒三定律开普勒第一定律——轨道定律所有行星都分别在大小不同的椭圆轨道上围绕太阳运动,太阳在这些椭圆的一个焦点上。开普勒第二定律——面积定律对每个行星来说,太阳和行星的连线在相等的时间扫过相等的面积。开普勒第三定律——周期定律所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等。行星32=akT我们的太阳系回顾历史,关于行星绕太阳运动的原因,哪些科学家提出了自己的解释?笛卡尔伽利略开普勒科学的足迹……一切物体都有合并的趋势行星的运动是受到了来自太阳的类似于磁力的作用,与距离成反比在行星的周围有旋转的物质(以太)作用在行星上,使得行星绕太阳运动胡克、哈雷等人认为行星受到了太阳对它的引力,甚至证明了如果行星的轨道是圆形的,其所受的引力大小跟行星到太阳的距离的平方成反比。胡克哈雷科学的足迹……FF太阳引力科学的足迹……如果太阳和行星间的引力与距离的二次方成反比,则行星的轨迹是椭圆。并且阐述了普遍意义下的万有引力定律。一、太阳对行星的引力追寻牛顿的足迹……设行星的质量为m,速度为v,行星到太阳的距离为r,则行星绕太阳做匀速圆周运动的向心力由太阳对行星的引力来提供2vFmr=天文观测难以直接得到行星的速度v,但可以得到行星的公转周期T2πrvT=代入得224πmrFT=追寻牛顿的足迹……32rkT=根据开普勒第三定律224πmFkr=所以太阳对不同行星的引力,与行星的质量成正比,与行星和太阳间的距离的二次方成反比。追寻牛顿的足迹……224πmFkr=太阳对行星的引力2mFrµ即根据牛顿第三定律,行星对太阳引力Fʹ应满足二、行星对太阳的引力追寻牛顿的足迹……2MFr¢µFFʹ行星太阳Mm则太阳与行星间的引力大小为G比例系数,与太阳、行星的质量无关三、太阳与行星间的引力方向:沿着太阳和行星的连线追寻牛顿的足迹……2mFrµFFʹ行星太阳Mm2MFr¢µ2MmFrµ2MmFGr=例1.火星绕太阳的运动可看作匀速圆周运动,火星与太阳间的引力提供火星运动的向心力。已知火星运行的轨道半径为r,运行的周期为T,引力常量为G,试写出太阳质量M的表达式。解:火星与太阳间的引力表达式为2MmFGr=由线速度与周期的关系2πrvT=22=MmvGmrr设火星运动的线速度为v,则324πrMGT=得太阳质量例2.两大小相同的实心小铁球紧靠在一起,它们之间的万有引力为F,若两个半径是小铁球2倍的实心大铁球紧靠在一起,则它们之间的万有引力为()A.F/4B.4FC.F/16D.16FD例3.一个质量均匀分布的球体,半径为2r,在其内部挖去一个半径为r的球形空穴,其表面与球面相切,如图所示。已知挖去小球的质量为m,在球心和空穴中心连线上,距球心d=6r处有一质量为m2的质点,求剩余部分对m2的万有引力。2241225mmGr例4.设想有一宇航员在某行星的极地上着陆时,发现物体在当地的重力是同一物体在地球上重力的0.01倍,而该行星一昼夜的时间与地球相同,物体在它赤道上时恰好完全失重。若存在这样的星球,它的半径R应多大?解:设行星的半径为R,在赤道上质量为m的物体随星体自转,物体受力如图所示,根据牛顿第二运动定律得mg′FN=mω2R依题意FN=0,所以g′=ω2R在极地地区物体重力仅为地球上重力的0.01倍,可知g′=0.01g自转周期与地球相同,即T′=T=8.64×104s222222472()0.014π4π0.019.88.6410m1.8510m43.14gTgTRg。例5.宇航员在地球表面以一定初速度竖直上抛一物体,经过时间t物体落回原处;若他在某星球表面以相同的初速度竖直上抛同一物体,需经过时间5t物体落回原处。(取地球表面重力加速度g=10m/s2,空气阻力不计)(1)求该星球表面附近的重力加速度g′的大小;(2)已知该星球的半径与地球半径之比为R星∶R地=14∶,求该星球的质量与地球质量之比M星∶M地。(1)2m/s2(2)180∶1.太阳对行星的引力2.行星对太阳的引力3.太阳与行星间的引力G是比例系数,与行星、太阳均无关引力的方向沿太阳和行星的连线2MFr¢µ2mFrµ2MmFGr=1.如图所示两球间的距离为r,两球的质量分布均匀,大小分别为m1、m2,半径分别为r1、r2,则两球间的万有引力大小为()D12212D.()mmGrrr12212C.()mmGrr122A.mmGr1221B.mmGr2.设想把质...