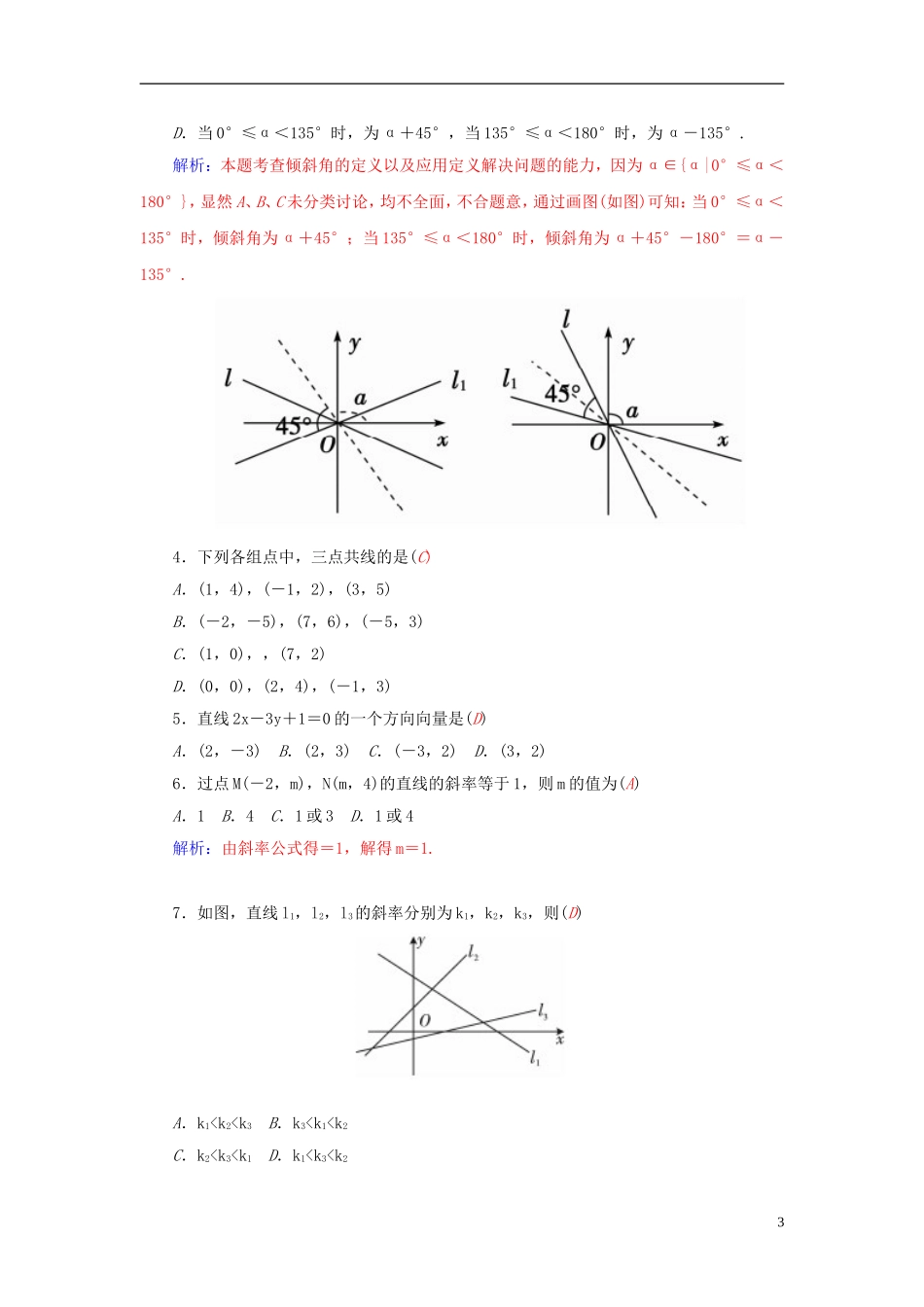
3.1.1倾斜角与斜率1.倾斜角与斜率.(1)倾斜角与斜率的概念.倾斜角斜率前提条件直线l与x轴相交倾斜角不是90°定义取x轴作为基准,x轴正向与直线l向上方向之间所成的角直线l倾斜角的正切值表示或记法αk=tanα(2)倾斜角与斜率的对应关系.图示倾斜角(范围)α=0°0°<α<90°α=90°90°<α<180°斜率(范围)0k>0斜率不存在k<0由上表可知直线l的倾斜角α的取值范围是0°≤α<180°,斜率k的取值范围是(-∞,+∞).当直线与x轴平行或重合时,我们规定它的倾斜角为0°.2.过两点的直线的斜率公式.直线过两点P1(x1,y1),P2(x2,y2),其斜率k=(x1≠x2).当直线倾斜角为90°时它的斜率不存在.α取值范围是[0,π).(1)直线的倾斜角α确定后,斜率k的值与点p1,p2的顺序是否有关?(2)当直线平行于y轴或与y轴重合时,上述公式k=还适用吗?答案:(1)无关.(2)不适用,因为此时斜率不存在.►思考应用1.表示直线倾斜程度的量有什么?解析:表示直线倾斜程度的量有直线的倾斜角和斜率,它们分别从“形”和“数”两方1面刻画了直线的倾斜程度.2.过两点P1(x1,y1)和P2(x2,y2)且x1=x2时,直线的倾斜角和斜率怎样?解析:此时直线的倾斜角为90°,斜率不存在.1.已知直线经过点A(0,4)和点B(1,2),则直线AB的斜率为(B)A.3B.-2C.2D.不存在解析:kAB==-2.2.已知直线l的倾斜角α=30°,则其斜率k的值为(B)A.0B.C.D.13.已知直线l的斜率k=-1,则其倾斜角为135°.1.直线l过(m,n),(n,m)两点,其中m≠n,mn≠0,则(D)A.l与x轴垂直B.l与y轴垂直C.l过原点和一、三象限D.l的倾斜角为135°解析:由斜率公式可得k1==-1,即tanα=-1,所以α=135°.故选D.2.以下四个命题错误的是(D)①若直线的斜率存在,则必有倾斜角与之对应;②若直线的倾斜角存在,则必有斜率与之对应;③坐标平面上所有的直线都有倾斜角;④坐标平面上所有直线都有斜率.A.①②B.③④C.①③D.②④3.设直线l过原点,其倾斜角为α,将直线l绕原点沿逆时针方向旋转45°,得到直线l1,则l1的倾斜角为(D)A.α+45°B.α-135°C.135°-α2D.当0°≤α<135°时,为α+45°,当135°≤α<180°时,为α-135°.解析:本题考查倾斜角的定义以及应用定义解决问题的能力,因为α∈{α|0°≤α<180°},显然A、B、C未分类讨论,均不全面,不合题意,通过画图(如图)可知:当0°≤α<135°时,倾斜角为α+45°;当135°≤α<180°时,倾斜角为α+45°-180°=α-135°.4.下列各组点中,三点共线的是(C)A.(1,4),(-1,2),(3,5)B.(-2,-5),(7,6),(-5,3)C.(1,0),,(7,2)D.(0,0),(2,4),(-1,3)5.直线2x-3y+1=0的一个方向向量是(D)A.(2,-3)B.(2,3)C.(-3,2)D.(3,2)6.过点M(-2,m),N(m,4)的直线的斜率等于1,则m的值为(A)A.1B.4C.1或3D.1或4解析:由斜率公式得=1,解得m=1.7.如图,直线l1,l2,l3的斜率分别为k1,k2,k3,则(D)A.k1α3,∴k2>k3>0,故选D.8.直线l的斜率为k,倾斜角是α,-1