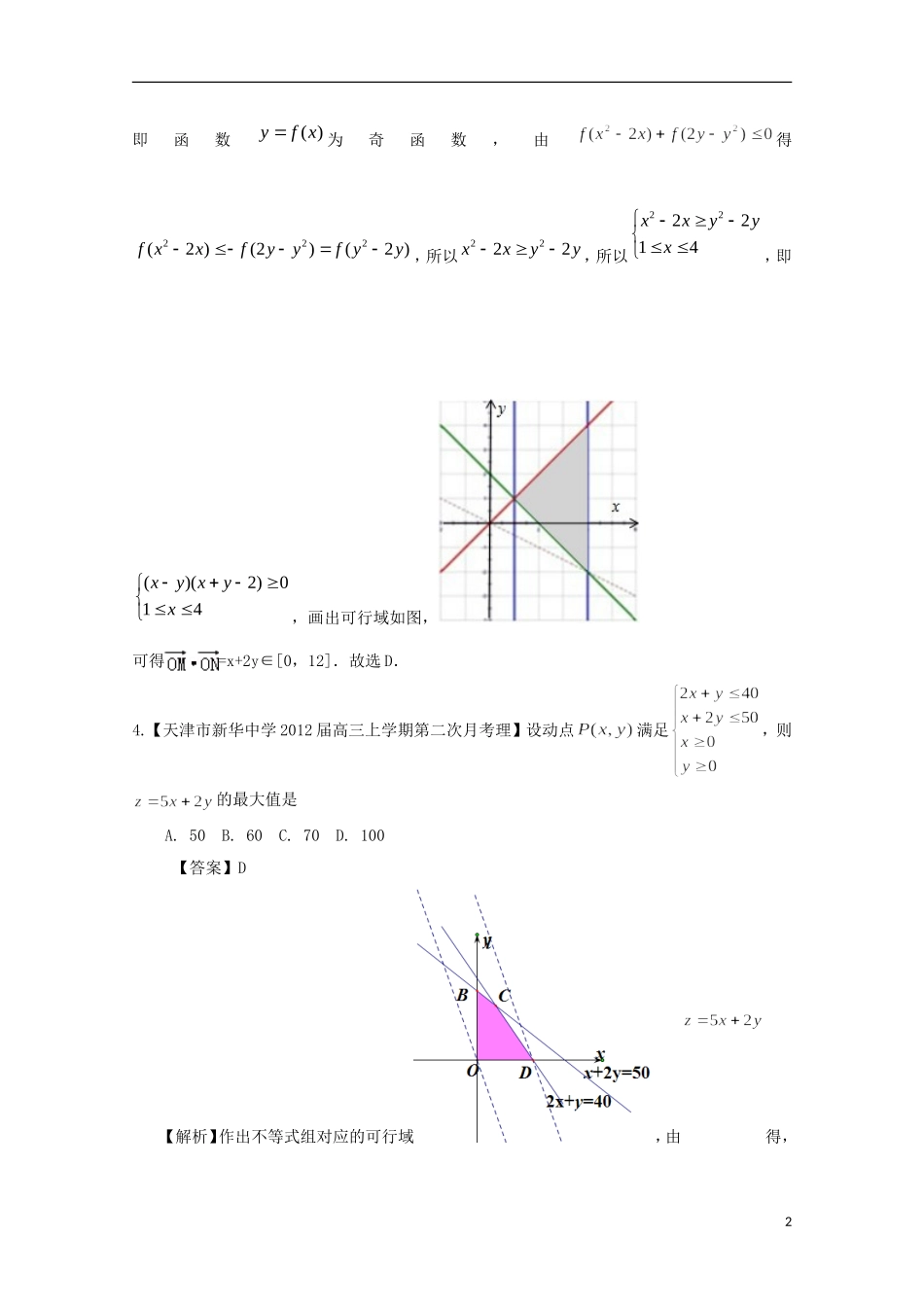
各地解析分类汇编:不等式1.【云南省玉溪一中2013届高三上学期期中考试理】已知向量,若,则的最小值为()A.B.12C.6D.【答案】C【解析】因为,所以,即,所以。则,当且仅当取等号,所以最小值为6,选C.2.【云南省玉溪一中2013届高三第四次月考理】关于的不等式的解为或,则点位于(A)第一象限(B)第二象限(C)第三象限(D)第四象限【答案】A【解析】由不等式的解集可知,是方程的两个根,且,不妨设,,所以,即点的坐标为,位于第一象限,选A.3.【云南省玉溪一中2013届高三第四次月考理】函数为定义在上的减函数,函数的图像关于点(1,0)对称,满足不等式,,为坐标原点,则当时,的取值范围为()A.B.C.D.【答案】D【解析】因为函数的图像关于点(1,0)对称,所以()yfx的图象关于原点对称,1即函数()yfx为奇函数,由得222(2)(2)(2)fxxfyyfyy,所以2222xxyy,所以222214xxyyx,即()(2)014xyxyx,画出可行域如图,可得=x+2y∈[0,12].故选D.4.【天津市新华中学2012届高三上学期第二次月考理】设动点满足,则的最大值是A.50B.60C.70D.100【答案】D【解析】作出不等式组对应的可行域,由得,2,平移直线,由图象可知当直线经过点时,直线的截距最大,此时也最大,最大为,选D.5.【山东省烟台市2013届高三上学期期中考试理】已知向量==,若,则的最小值为A.B.C.D.【答案】C【解析】由题意知.故选C.6.【云南师大附中2013届高三高考适应性月考卷(三)理科】已知函数则满足不等式的x的取值范围为()A.B.(-3,0)C.(-3,1)D.(-3,-)【答案】B【解析】由函数图象可知,不等式的解为即,故选B.7.【山东省实验中学2013届高三第一次诊断性测试理】设x、y满足则A.有最小值2,最大值3B.有最小值2,无最大值C.有最大值3,无最大值D.既无最小值,也无最大值【答案】B3【解析】做出可行域如图(阴影部分)。由得,做直线,平移直线由图可知当直线经过点C(2,0)时,直线的截距最小,此时z最小为2,没有最大值,选B.8.【山东省烟台市莱州一中20l3届高三第二次质量检测(理)】设变量满足约束条件的取值范围是A.B.C.D.【答案】C【解析】做出约束条件表示的可行域如图,由图象可知。的几何意义是区域内的任一点到定点的斜率的变化范围,由图象可知,,所以,即,所以取4值范围是,选C.9.【山东省师大附中2013届高三12月第三次模拟检测理】若实数满足不等式组则的最大值是()A.11B.23C.26D.30【答案】D【解析】做出可行域如图,设,即,平移直线,由图象可知当直线经过点D时,直线的截距最大,此时z最大。由0,2100,xyxy解得10,10,xy,即(10,10)D,代入得,所以最大值为30,选D.10【北京市东城区普通校2013届高三12月联考数学(理)】设变量yx,满足约束条件01042022xyxyx,则目标函数xyz32的最大值为A.3B.2C.4D.5【答案】C5【解析】做出约束条件对应的可行域如图,,由得。做直线,平移直线得当直线经过点时,直线的截距最大,此时最大,所以最大值,选C.11【云南师大附中2013届高三高考适应性月考卷(三)理科】实数对(x,y)满足不等式组则目标函数z=kx-y当且仅当x=3,y=1时取最大值,则k的取值范围是()A.B.C.D.【答案】C【解析】不等式组所表示的区域如图2所示,直线zkxyykxz过(31),时z取最大值,即直线ykxz在y轴上的截距z最小,由图可得直线ykxz的斜率112k,,故选6C.12【北京市东城区普通校2013届高三12月联考数学(理)】若0,0,2abab,则下列不等式对一切满足条件的,ab恒成立的是.(写出所有正确命题的编号).①1ab;②2ab;③222ab;④333ab;⑤112ab【答案】①,③,⑤.【解析】对于命题①由,得,命题①正确;对于命题②令时,不成立,所以命题②错误;对于命题③,命题③正确;对于命题④令时,不成立,所以命题④错误;对于命题⑤,命题⑤正确.所以正确的结论为①,③,⑤.13【山东省济南外国语学校2013届高三上学期期中考试理科】已知x和...