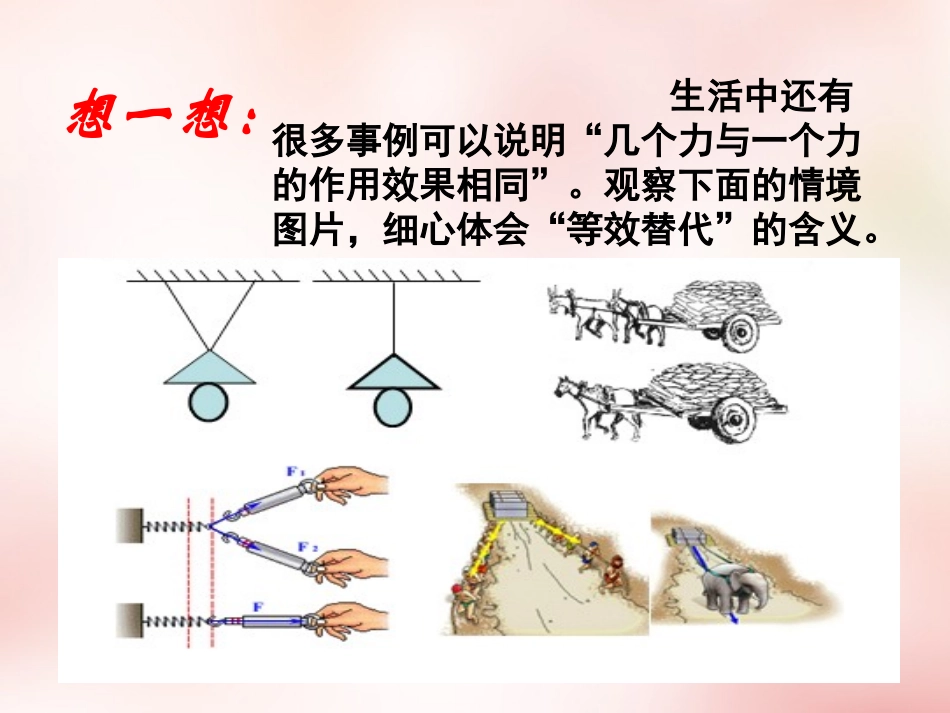
G=200NF1F2G=200N观察下面的情境图片,结合生活经验思考:两位小孩对水桶施加的两个力与一位大人对水桶施加的一个力,就“提起水桶”这一作用效果而言,相同吗?它们可以相互替代吗?说出你的看法。请自由发言。生活中还有很多事例可以说明“几个力与一个力的作用效果相同”。观察下面的情境图片,细心体会“等效替代”的含义。想一想:第4节、力的合成1、定义:若一个力作用在物体上,所产生的效果跟几个力共同作用产生的效果相同,则这个力叫那个力的合力,而那几个力叫这个力的分力.F为F1、F2的合力;F1、F2为F的分力。2、合力与分力的关系:(1)合力与分力是作用效果上的一种等效替代关系(2)合力是几个分力的共同效果,并不是单独存在的力,因此受力分析中不能同时出现。一.合力与分力二、力的合成:力的合成是惟一的;只有同一物体所受的力才可合成;不同性质的力也可以合成;分力与合力从物理实质上讲是在力的作用效果方面的一种等效替代关系,而不是物体的重复受力.力的合成应注意以下问题:(1)定义:求几个力的合力的过程,叫做力的合成.(2)实质:就是找一个力去替代作用在物体上的几个已知的力,而不改变其作用效果。1、同一直线上二力的合成(回顾初中知识)同向:反向:2、探究实验:不在一条直线上的二力的合力的大小还等于两分力大小之和或之差吗?不等于要研究它们之间的关系,就很有必要将合力与分力的大小和方向一同表示出来,那么用什么形式来表示力的大小和方向?力的图示F1F2F1F2F合F合互成角度的二力的合成F合=F1+F2F合=│F1-F2│1.如何确定两个分力的大小和方向?器材有:橡皮条、细绳套、弹簧测力计两个过程:用两个弹簧测力计互成角度拉橡皮条到结点,再改用一个弹簧测力计拉橡皮条到同一结点。2.三个力的图示起端点画在一起,再将它们的箭头端点用虚线连接起来,看看图形像四边形?怎么样来检验它是平行四边形?3.代表分力的有向线段都处在平行四边形中的什么位置?是一组对边还是一组邻边?4.代表合力的有向线段处于平行四边形中的什么具体位置?5.改变分力的大小和方向,多做两次,结果一样吗?你能得出什么结论?F1=10.0NF2=6.8NF合=12.8NO2N实验探究实验探究三、平行四边形定则(1)定义:如果用表示两个共点力F1和F2的线段为邻边作平行四边形,那么,合力F的大小和方向就可以用这两个邻边之对角线表示出来,这叫做力的平行四边形定则.标量是简单的加减运算矢量不是简单的加减运算,平行四边形定则是所有的矢量合成都遵循的普遍规律F1F合F2θ(2)应用平行四边形定则时注意四点:①分力、合力的起点相同②分力、合力的标度比例一致③虚、实要分清,力画实线,辅助线画虚线④求合力时既要得出合力的大小还要得出力的方向α1、求二个力的合力的方法⑴同一直线上两个力的合成先选取正方向,再赋予矢量正负值,化矢量运算为代数运算求得矢量和。如得正值则合力沿正方向,如得负值则合力方向与所选取的正方向相反例题三⑵互成角度的两个力的合成①作图法ⅲ根据分力的标度量得对角线的长度就代表了合力的大小,对角线与任一分力的夹角就代表合力的方向ⅱ以F1、F2为邻边作平行四边形,从而得到F1、F2之间的对角线ⅰ根据两个力的大小和方向,按一定的标度用力的图示从力的作用点起作出两个分力F1、F2②计算法可以根据平行四边形定则作出的示意图,然后根据正、余弦定理,三角函数等几何知识计算合力。若两个分力大小为F1、F2,它们之间的夹角为α,则:F1F合F2θααF2sinαF2cosαF1+F2cosα22221sincosFFFF合合力的大小cossintan212FFF合力的方向cos2212221FFFF┍若两个分力大小为F1=F2=F,它们之间的夹角为α,那么力的合成作出的平行四边形是菱形,菱形的对角线垂直平分,则有:2cos2FF合合力的大小02F603F902F120F1800F1F2F合αα/2两个力的合成可用力平行四边形定则,那么多于两个的力怎么合成呢?2、平行四边形定则的应用扩展三个力的合成可以先求任两个的合力,再将这合力与第三个力合成求出三个力的合力。F1F2F3F合F12课外思考:多边形定则3、三角形...