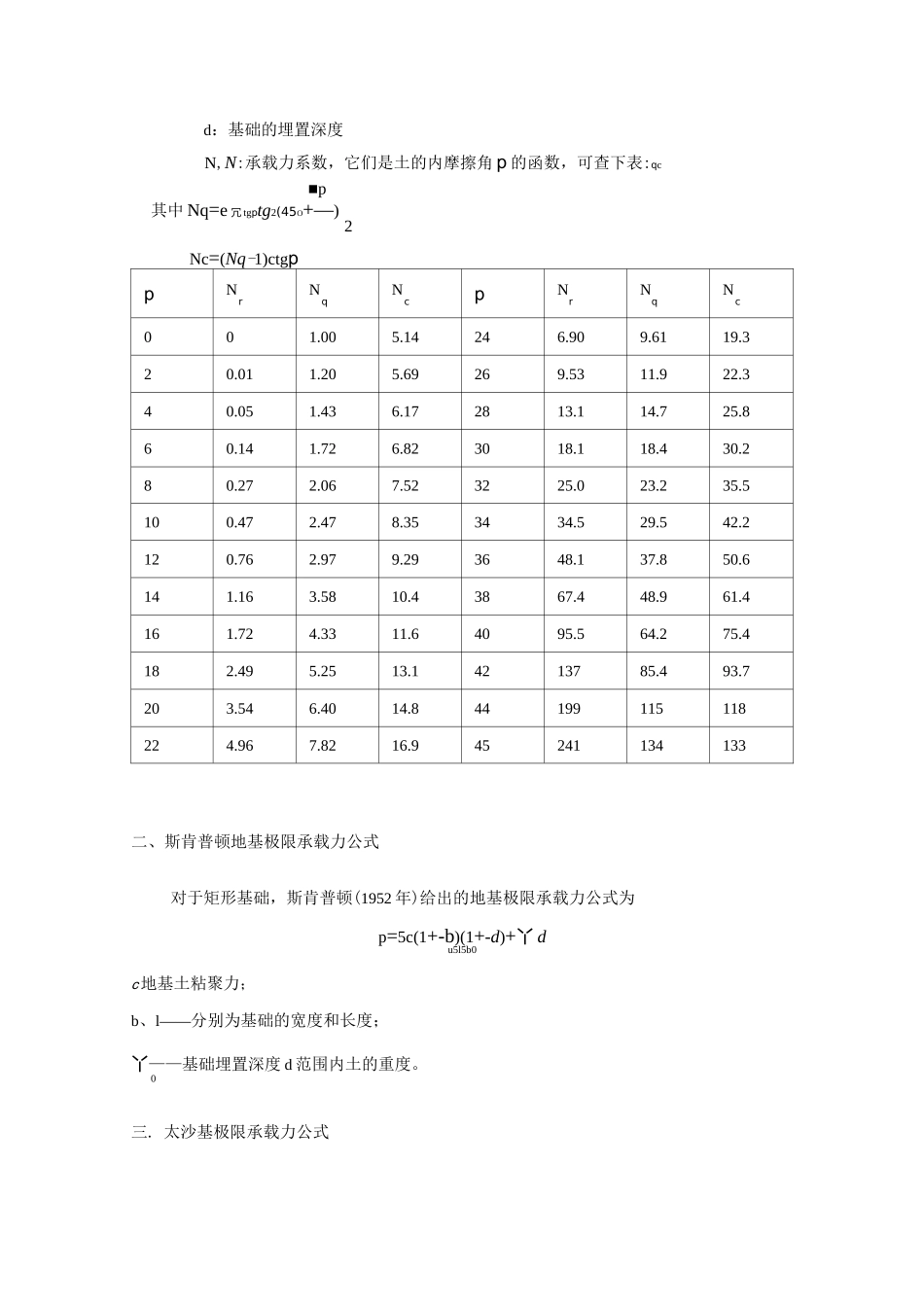
第三节极限承载力的计算在土力学的发展中,已经提出了许多极限荷载公式,1920年普朗特首先根据塑性平衡理论导出了介质达到极限荷载时,沿着曲面发生滑动的数学方程,并认为介质的抗剪强度性质,可以用强度指标c,p表示,但是,他的研究结果只适用于无重量的介质的极限平衡平面课题。随后不少学者根据他的研究结果,引用来求解地基土的极限荷载,并进一步作了不同形式的修正和补充,以便在工程中加以应用。太沙基根据普朗特相似的概念,导出了考虑地基土自重影响的极限荷载公式。但这些公式都忽略了基础底面以上覆盖土层的抗剪强度的影响,故只适用于计算浅基础的极限荷载。梅耶霍夫进一步考虑了基础底面以上覆盖层的抗剪强度的影响,从而提出了浅基础和深基础的极限荷载公式。一.普朗特尔极限承载力公式普朗特尔公式是求解宽度为b的条形基础,置于地基表面,在中心荷载P作用下的极限荷载Pu值。普朗特尔的基本假设及结果,归纳为如下几点:(1)地基土是均匀,各向同性的无重量介质,即认为土的丫二0,而只具有c,p的材料。(2)基础底面光滑,即基础底面与土之间无摩擦力存在,所以基底的压应力垂直于地面。(3)当地基处于极限平衡状态时,将出现连续的滑动面,其滑动区域将由朗肯主动区I,径向剪切区II或过渡区和朗肯被动区III所组成。其中滑动区I边界BC或AC为直线,并与水平面成(45+P/2)角;即三角形ABC是主动应力状态区;滑动区II的边界CE或CD为对数螺旋曲线,其曲线方程为r=re$g0,r0为起始矢径;0为射线r与r0夹角,滑000动区III的边界EG,DF为直线并与水平面成(45—Q/2)角。(4)当基础有埋置深度d时,将基础底面以上的两侧土体用相当的均布超载q=yd来代替。根据上述的基本假设,采用刚体平衡方法或特征线法,可以得到地基极限承载力为:p=rdN+cNuqc式中:r:基础两侧土的容重d:基础的埋置深度N,N:承载力系数,它们是土的内摩擦角p的函数,可查下表:qc■p其中Nq=e冗tgptg2(45O+—)2Nc=(Nq-1)ctgppNrNqNcpNrNqNc001.005.14246.909.6119.320.011.205.69269.5311.922.340.051.436.172813.114.725.860.141.726.823018.118.430.280.272.067.523225.023.235.5100.472.478.353434.529.542.2120.762.979.293648.137.850.6141.163.5810.43867.448.961.4161.724.3311.64095.564.275.4182.495.2513.14213785.493.7203.546.4014.844199115118224.967.8216.945241134133二、斯肯普顿地基极限承载力公式对于矩形基础,斯肯普顿(1952年)给出的地基极限承载力公式为p=5c(1+-b)(1+-d)+丫du5l5b0c地基土粘聚力;b、l——分别为基础的宽度和长度;丫——基础埋置深度d范围内土的重度。0三.太沙基极限承载力公式+qN+cNqcN称为承载力系数,都是土的内摩擦角P的函对于均匀地基上的条形基础,当受中心荷载作用时,若把土作为有重量的介质,即Y不等于零,求其极限承载力时,太沙基作了如下假设:1.基础底面粗糙,即的与土之间有摩擦力存在当地基达到破坏并出现连续的滑动面时其基底下有一部分土体将随着基础一起移动而处于弹性平衡状态,该部分土体称为弹性核或叫弹性契体,如图8-9中ABC所示。弹性核的边界AC或BC为滑动面的一部分,它与水平面的夹角为P,而它的具体数值又与基底的粗糙程度有关。2.当把基底看作是完全粗糙时,则滑动区域由径向过渡区剪切区II和朗肯被动区III所组成。其中滑动区域II的边界CE和DC为对数螺旋曲线,其曲线方程为(r0为起始矢径)。朗肯区域III的边界DFA为直线,它与水平面成(45。一Q/2)角。3.当基础有埋置深度时,则基底以上两侧的土体用相当的均布超载q=yd来代替。根据上述假定,经推导可得地基的极限承载力1p二rbNu2式中:N,N,rq其中:Nq=①2COS2(45O+2)Nc-(Nq一1)ctg甲但对N,太沙基并未给出公式。太沙基将N,N,N可以查表8—4得。rrqc几点说明:(1)当把基础底面假定为光滑时,则基底以下的弹性核就不存在,而成为朗肯主动区I了,而AC面与水平面的夹角屮=(45。+屮/2)而整个滑动区域将完全与普朗特尔的情况相似,因此,由C,q所引起的承载力系数即可直接取用普朗特尔的结果,即:N=e冗tg®tg2(45o+)q2N=(Nq一1)ctg®c而由土容重Y所引起的承载力系数则采用...