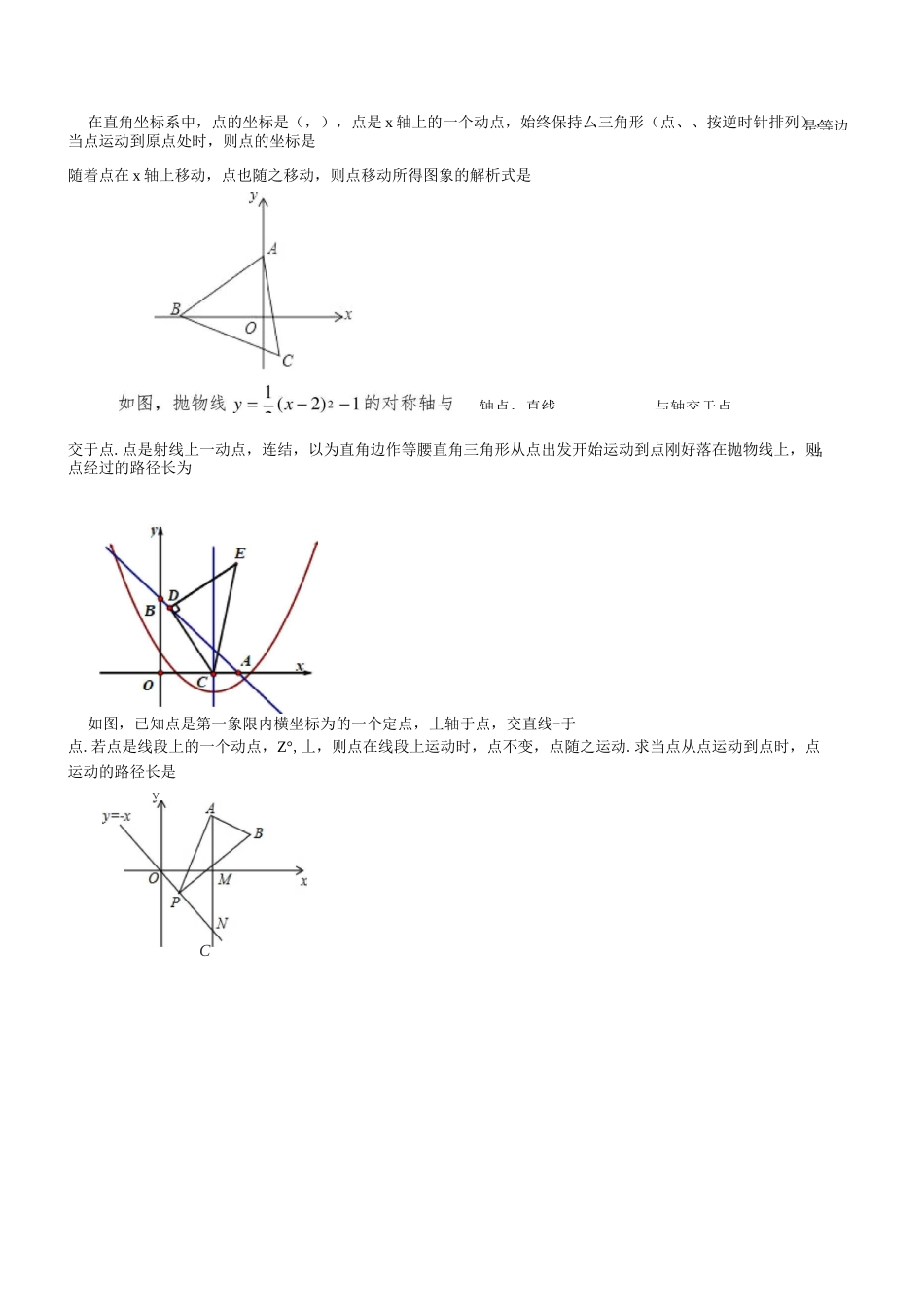
BQ相似三角形提高一、相似三角形动点问题如图,在△中,Z°,,,过点作射线]〃.动点从点出发沿射线方向以每秒个单位的速度运动,同时动点从点沿射线方向以每秒个单位的速度运动.过点作丄于,过点作丄交射线于,是中点,连接.设点运动的时间为秒.()当为何值时,,并求出此时的长度;()当厶与厶相似时,求的值.CDE如图,在厶中,Z=°,,,动点以的速度从点出发,沿向点移动.同时,动点以的速度从点出发,沿向点移动.当其中有一点到达终点时,它们都停止移动.设移动的时间为秒.()①当时,求厶的面积;②求△的面积(平方米)关于时间(秒)的函数解析式;()在,移动的过程中,当厶为等腰三角形时,求出的值.的速度移()表如图,在矩形中,,,点沿边从开始向点以动;点沿边从点开始向点以的速度移动.如果、同时出发,示移动的时间(VV)。()当为何值时,△为等腰直角三角形?()当为何值时,以点、、为顶点的三角形与△相似?以每秒当点到达如图所示,在厶中,==,=,点从点出发,沿着的速度向点运动;同时点从点出发,沿以每秒的速度向点运动,点时,点随之停止运动.设运动的时间为.()当为何值时,〃?()△与厶能否相似?若能,求出的长;若不能说明理由.如图,在△中,Z=°,=,=,点在边上运动,交边于点,丄,垂足为,丄,垂足为.()当=时,求证:〃;()探究:为何值时,△与厶相似?CB当与轴交于点是等边在直角坐标系中,点的坐标是(,),点是x轴上的一个动点,始终保持厶三角形(点、、按逆时针排列),当点运动到原点处时,则点的坐标是随着点在x轴上移动,点也随之移动,则点移动所得图象的解析式是交于点.点是射线上一动点,连结,以为直角边作等腰直角三角形从点出发开始运动到点刚好落在抛物线上,则点经过的路径长为如图,已知点是第一象限内横坐标为的一个定点,丄轴于点,交直线-于点.若点是线段上的一个动点,Z°,丄,则点在线段上运动时,点不变,点随之运动.求当点从点运动到点时,点运动的路径长是轴点,直线VC的图象与线段的夹角在厶中,245,三角形,求线段的长.,以为边在点的异侧作△,使△为等腰直角在厶中,,z折叠,°,点是上的一点,点是上的点.求证:::.上的一点,沿着直线如图,在直角坐标系中,矩形的边在轴上,边在翻折点落在点的位置,且交轴于点213113(-2,13)(--,13)轴上,点的坐标为(,.那么点的坐标为()312(-3,上)55二、构造相似辅助线一一双垂直模型在平面直角坐标系中,点的坐标为,,正比例函数是°,求这个正比例函数的表达式.),将矩形沿对角为短边在第一象限做一个矩已知,如图,直线-+与坐标轴交于、两点.以形,使得矩形的两边之比为:。求、两点的坐标。三、构造相似辅助线一一、字型如图:△中,是上一点,,边上的中线交于。求证:四边形中,为的比例中项,且平分Z求证:22B:重心是三、b和k表示请你猜想用aDE当DE=k时,参照上述研究结论,a+3b3当竺=2时,AE当匹=1时,出;AE2当匹=3时,空AE4在梯形中,〃,=,=,为边上的任意一点,〃于点,某同学在研究这一问题时,发现如下事实:的一般结论,并给出证明.已知:如图,在厶中,是的中点,、是上的两点,且二求::.2证明:重心定理:三角形顶点到重心的距离等于该顶点对边上中线长的亍角形三条中线的交点)为上任意一点,、的延四、相似类定值问题分别是边,的中点,如图,在等边厶中,长线分别交、于点、1,1_3求证:CS+~BF~AB,如图,在厶中,已知为边上的高,正方形的四个顶点分别在△上。已知:如图,梯形中,,对角线、交于,过作分别交111+=—ABCDEO求证:求证:ABCDEFFDGB是中线,是上一点,过作〃,延长交已知’在厶中作内接菱形,设菱形的边长为a•求证:-AC+Be=a.五、相似之共线线段的比例问题()如图,点在平行四边形的对角线上,一直线过点分别交,的延长线于点,,交于点.求证:•()如图,图,当点在平行四边形的对角线或的延长线上时,・是否仍然成立?若成立,试给出证明;若不成立,试说明理由(要求仅以图为例进行证明或说明);图1图2已知:如图,△中,=于,交于.求证:2=BDC如图,已知△中,,,交延长线于。求证:分别为,2•边上的高,过作的垂线交于,交已知如图,为平行四边形的延...