高一数学3.3 幂函数 3.4 函数的应用（II）人教实验版（B）VIP免费

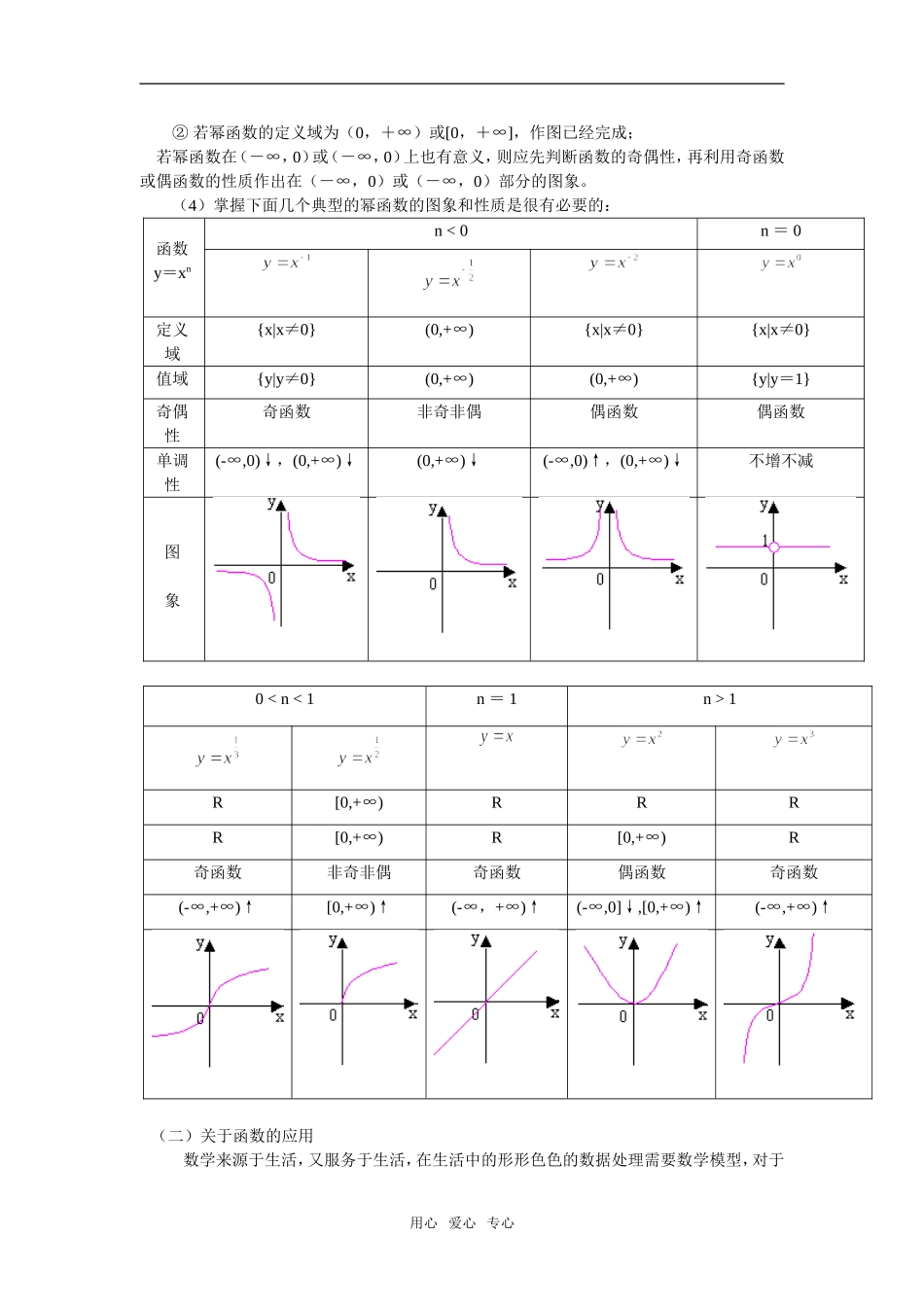
高一数学3.3幂函数3.4函数的应用（II）人教实验版（B）【本讲教育信息】一.教学内容：3.3幂函数3.4函数的应用（II）二.教学目的1、通过实例，了解幂函数的概念；结合函数的图象，了解它们的变化情况。2、利用计算工具比较指数函数，对数函数以及幂函数的增长差异，结合实例体会直线上升、指数爆炸、对数增长等不同函数类型增长的含义。3、收集一些社会生活中普遍使用的函数模型（指数函数、对数函数、幂函数）的实例，了解函数模型的广泛应用。三.教学重点、难点重点：（1）幂函数的定义、图象和性质（2）建立数学模型难点：（1）幂函数的图象的位置和形状变化（2）建立数学模型四.知识分析（一）关于幂函数1.幂函数的定义：一般地，我们把形如的函数称为幂函数，其中x是自变量，a是常数。①在这里我们只讨论a是有理数时的简单的幂函数。②掌握幂函数的关键一定要明确“形如的函数”这句话的重要作用。函数“”等都是幂函数，而象“”等就不是幂函数。足见幂函数对格式要求之严格。③对于幂函数的定义域和值域是由它的幂指数来确定的，幂指数不同，定义域和值域也不同：（1）当指数n是正整数时，定义域是R。（2）当指数n是正分数时，设（p,q是互质的正整数，q>1），则。如果q是奇数，定义域是R；如果q是偶数，定义域是[0,＋∞)。（3）当指数n是负整数时，设显然x不能为零，所以定义域是（4）当指数n是负分数时，设（p,q是互质的正整数，q>1），则。如果q是奇数，定义域是；用心爱心专心如果q是偶数，定义域是（0,＋∞）。2.幂函数的图象与性质幂函数部分的内容是学习的难点，要突破这个难点，关键是如何快速地画出能基本反映幂函数图象特征的草图，因为有了草图，有关幂函数的定义域、值域、单调性、奇偶性等函数性质就会一目了然，而且也有利于培养、形成数形结合的思维习惯。（1）第一象限内图象规律总结（结合图形）：①n>1时，过（0，0）、（1，1）的抛物线型，下凸递增。②n＝1时，过（0，0）、（1，1）的射线。③01的图象都在③号部分里，分布得相当有规律。在直线x＝1的左侧，同样有类似的规律，同学们可以自己发现。其实有上面的规律足够用了。（2）整个图象的规律：设（p,q是互质，p∈Z，q∈N）①任何幂函数在第一象限必有图象，在第四象限必无图象；②时，函数非奇非偶，只在第一象限有图象；③时，函数是偶函数，图象在第一、二象限都有图象（坐标轴上也可能有）并关于y轴对称。④时，函数是奇函数，图象在第一、三象限都有图象（坐标轴上也可能有）并关于原点对称。（3）快速作幂函数图象的步骤：不管n取什么有理数，幂函数的公共定义域为（0，＋∞），可见幂函数在第一象限内总有图象，因此作幂函数图象应先从第一象限入手：①先作出第一象限内的图象；用心爱心专心②若幂函数的定义域为（0，＋∞）或[0，＋∞]，作图已经完成；若幂函数在（－∞，0）或（－∞，0）上也有意义，则应先判断函数的奇偶性，再利用奇函数或偶函数的性质作出在（－∞，0）或（－∞，0）部分的图象。（4）掌握下面几个典型的幂函数的图象和性质是很有必要的：函数y＝xnn<0n＝0定义域{x|x≠0}(0,+∞){x|x≠0}{x|x≠0}值域{y|y≠0}(0,+∞)(0,+∞){y|y＝1}奇偶性奇函数非奇非偶偶函数偶函数单调性(-∞,0)↓，(0,+∞)↓(0,+∞)↓(-∞,0)↑，(0,+∞)↓不增不减图象01R[0,+∞)RRRR[0,+∞)R[0,+∞)R奇函数非奇非偶奇函数偶函数奇函数(-∞,+∞)↑[0,+∞)↑(-∞，+∞)↑(-∞,0]↓,[0,+∞)↑(-∞,+∞)↑（二）关于函数的应用数学来源于生活，又服务于生活，在生活中的形形色色的数据处理需要数学模型，对于用心爱心专心事物的发展和预测也离不开数学模型的建立，所以数学模型是提出问...