北京四中高考数学总复习 空间几何体结构及其三视图基础巩固练习VIP免费

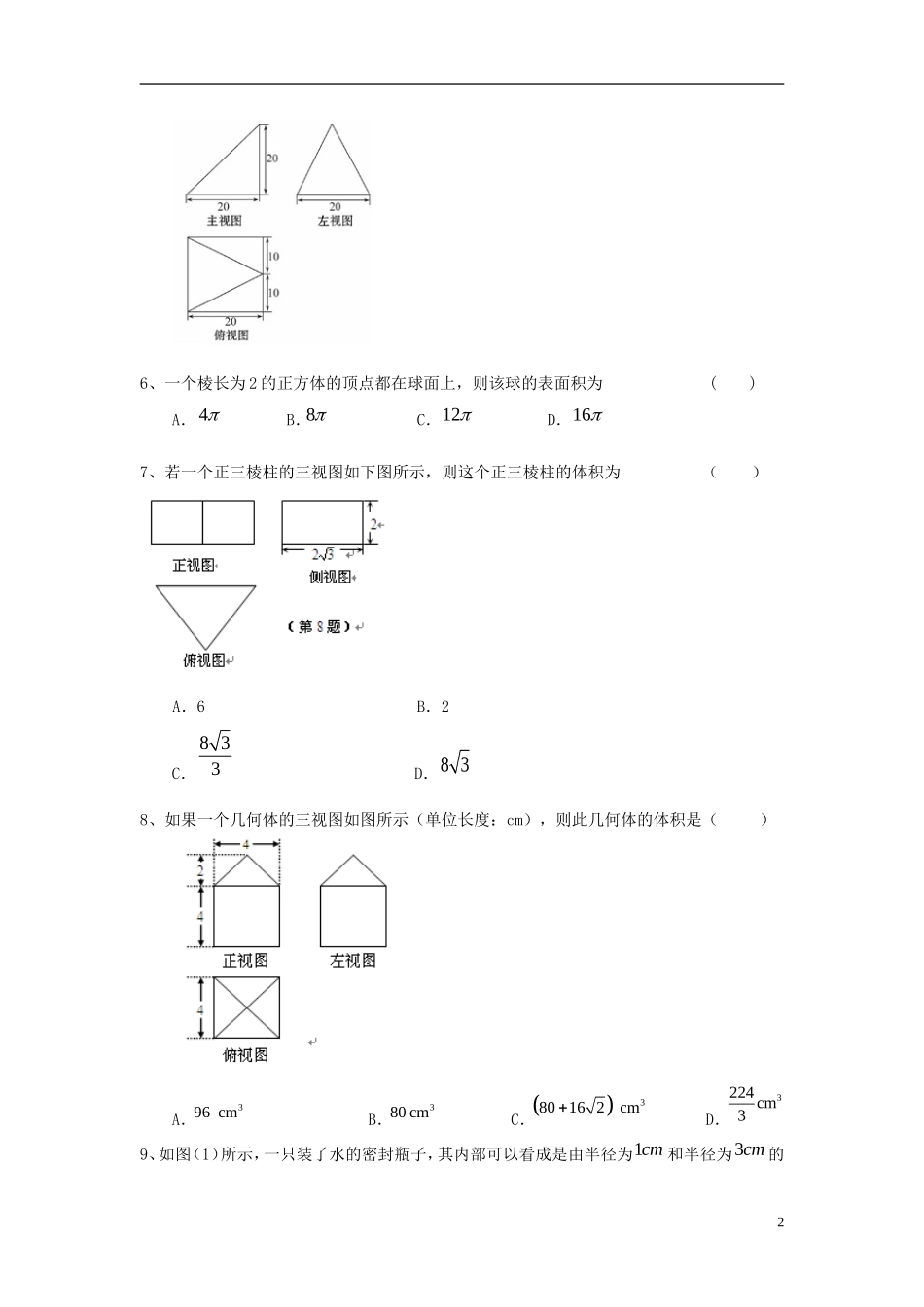
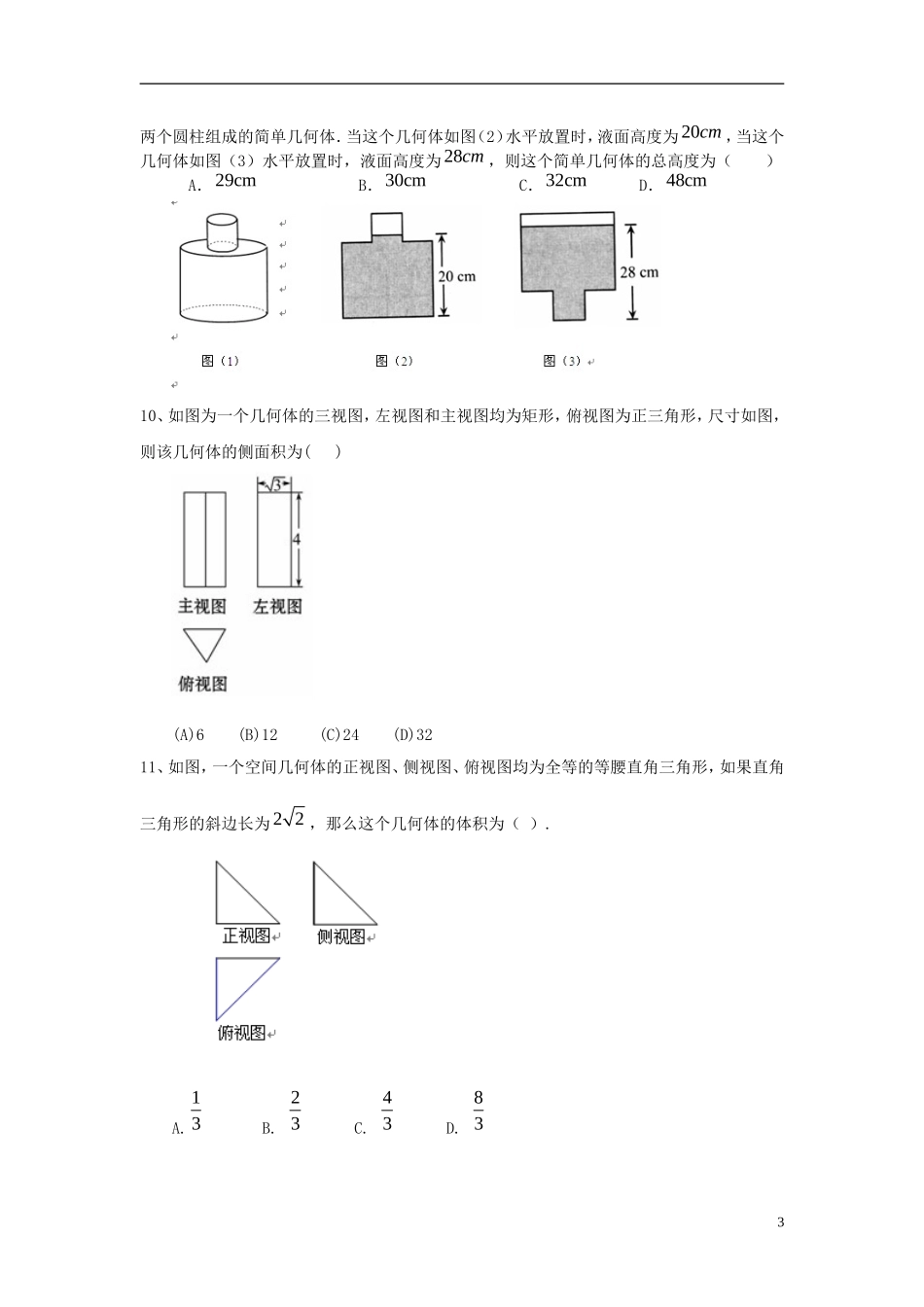
北京四中高考数学总复习空间几何体结构及其三视图基础巩固练习【巩固练习】1、若正方体的棱长为2，则以该正方体各个面的中心为顶点的凸多面体的体积为（）(A)26(B)23(C)33(D)232、圆柱的侧面展开图是一个边长为6π和4π的矩形，则该圆柱的底面积是()(A)24π2(B)36π2(C)36π2或16π2(D)9π或4π3、如图，某几何体的主视图与左视图都是边长为1的正方形，且体积为，则该几何体的俯视图可以是()4、如图是一几何体的三视图，其左视图是等腰直角三角形，则其表面积为（）A．262B．244C．246D．125、已知某个几何体的三视图如图所示，根据图中标出的尺寸(单位：cm)，可得这个几何体的体积是()16、一个棱长为2的正方体的顶点都在球面上，则该球的表面积为()A．4B．8C．12D．167、若一个正三棱柱的三视图如下图所示，则这个正三棱柱的体积为（）A．6B．2C．833D．838、如果一个几何体的三视图如图所示（单位长度：cm），则此几何体的体积是（）A．396cmB．380cmC．380162cmD．3224cm39、如图（1）所示，一只装了水的密封瓶子，其内部可以看成是由半径为1cm和半径为3cm的2两个圆柱组成的简单几何体．当这个几何体如图（2）水平放置时，液面高度为20cm，当这个几何体如图（3）水平放置时，液面高度为28cm，则这个简单几何体的总高度为（）A．29cmB．30cmC．32cmD．48cm10、如图为一个几何体的三视图，左视图和主视图均为矩形，俯视图为正三角形，尺寸如图，则该几何体的侧面积为()(A)6(B)12(C)24(D)3211、如图，一个空间几何体的正视图、侧视图、俯视图均为全等的等腰直角三角形，如果直角三角形的斜边长为22，那么这个几何体的体积为（）.A.13B.23C.43D.83312、若一个圆锥的侧面展开图是面积为2的半圆面,则该圆锥的体积为_________13、直三棱柱111ABCABC的各顶点都在同一球面上，若12ABACAA,120BAC，则此球的表面积等于。14、正三棱柱111ABCABC内接于半径为2的球，若,AB两点的球面距离为，则正三棱柱的体积为．15、如图是一个几何体的三视图，该几何体的体积为8，则a的值为______.【参考答案与解析】1、【答案】B.【解析】由题意知以正方体各个面的中心为顶点的凸多面体为正八面体（即两个同底同高同棱长的正四棱锥），所有棱长均为1，其中每个正四棱锥的高均为22，故正八面体的体积为21222=21=323VV正四棱锥,故选B.2、【答案】D.【解析】由题意知圆柱的底面圆的周长为6π或4π，故底面圆的半径为3或2，所以底面圆的面积是9π或4π.3、【答案】C.【解析】由该几何体的主视图和左视图可知该几何体是柱体，且其高为1，由其体积是可知该几何体的底面积是，由图知A的面积是1，B的面积是，C的面积是，D的面积是，故选C.4、【答案】C5、【答案】B.4【解析】由三视图知该几何体是如图所示的四棱锥P-ABCD，其中侧面PBC⊥底面ABCD，且顶点P在底面的射影是BC边的中点，四棱锥的高为20，底面ABCD是边长为20的正方形.∴VP-ABCD=×202×20=(cm3).6、【答案】C7、【答案】D.8、【答案】D.9、【答案】A.10、【答案】C.【解析】由几何体的三视图可知，该几何体为正三棱柱，其底面边长为2，高为4，∴该几何体的侧面积S侧=3×2×4=24.11、【答案】C.二、填空题12、【答案】【解析】如图,l=2,又2r2=l=2r=1,所以h=,故体积.13、【答案】2420R【解析】在ABC中2ABAC,120BAC,可得23BC,由正弦定理,可得ABC外接圆半径r=2,设此圆圆心为O，球心为O，在RTOBO中，易得球半径5R，故此球的表面积为2420R。14、【答案】8【解析】由条件可得2AOB，所以22AB，O到平面ABC的距离为233，所以所5POrlhPl2r求体积等于8．15、【答案】3【解析】由三视图知，该几何体是三棱锥，其直观图如图所示.其中PA、AB、AC两两互相垂直，∴V=×4×4×a=8,∴a=3.6