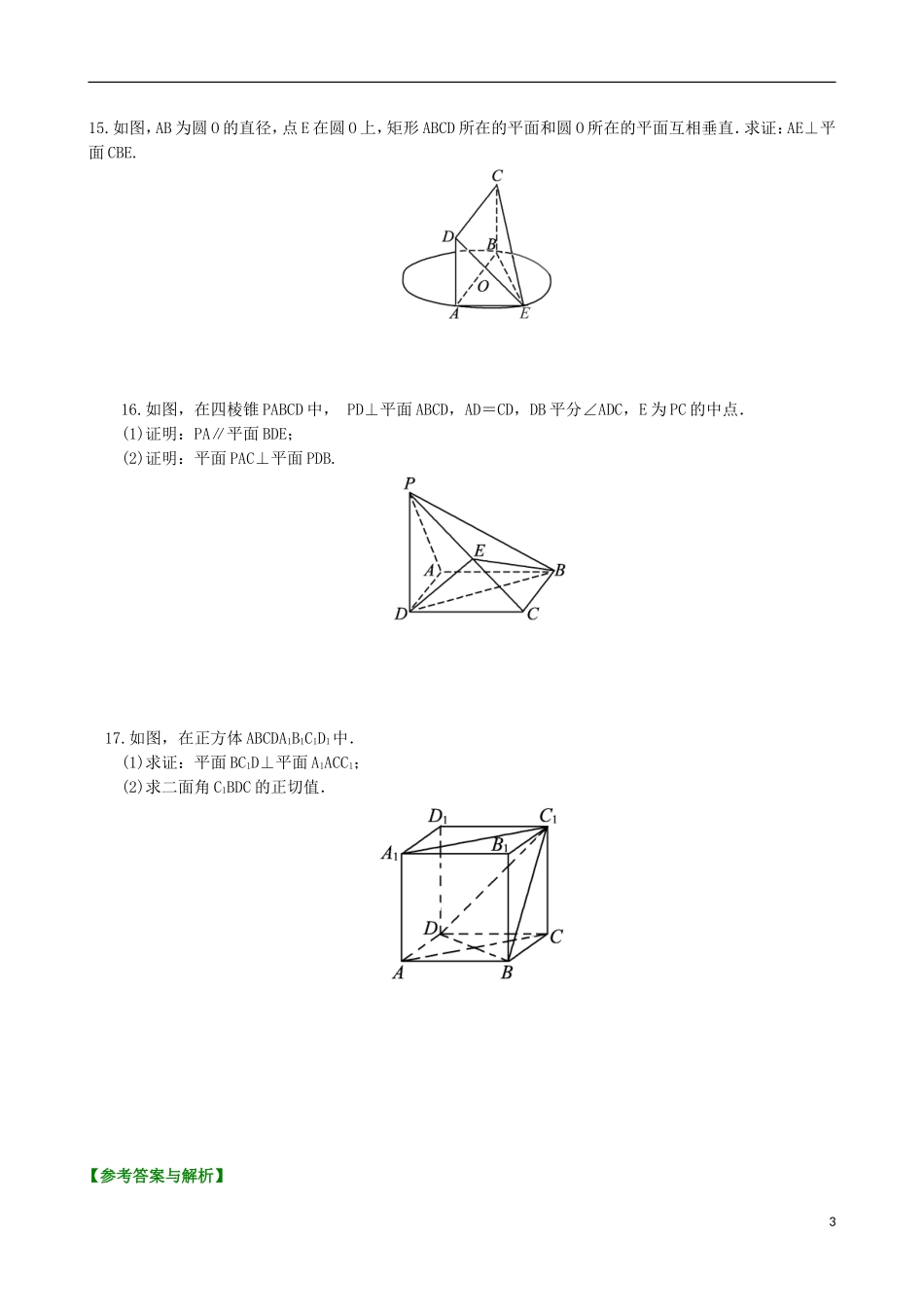
北京四中高考数学总复习直线、平面垂直的判定和性质基础巩固练习【巩固练习】1.直线与平面α内无数条直线垂直是“直线与平面α垂直”的________条件(填“充分不必要”、“必要不充分”、“充要”“既不充分也不必要”).2.关于直线m,n和平面α,β,有以下四个命题:①若m∥α,n∥β,α∥β,则m∥n;②若m∥n,m⊂α,n⊥β,则α⊥β;③若α∩β=m,m∥n,则n∥α且n∥β;④若m⊥n,α∩β=m,则n⊥α或n⊥β.其中假命题的序号是________.3.设l,m是两条不同的直线,α是一个平面,则下列命题正确的有________.①若l⊥m,m⊂α,则l⊥α;②若l⊥α,l∥m,则m⊥α;③若l∥α,m⊂α,则l∥m;④若l∥α,m∥α,则l∥m.4.设b,c表示两条直线,α,β表示两个平面,现给出下列命题:①若b⊂α,c∥α,则b∥c;②若b⊂α,b∥c,则c∥α;③若c∥α,α⊥β,则c⊥β;④若c∥α,c⊥β,则α⊥β.其中正确的命题是________.(写出所有正确命题的序号)5.已知直线a,b与平面α,β,γ,能使α⊥β的条件是________.(填序号)①α⊥γ,β⊥γ;②α∩β=a,b⊥a,b⊂β;③a∥α,a∥β;④a⊥β,a∥α.6.设m,n是两条不同的直线,α、β、γ是三个不同的平面,给出下列命题:①若m⊂β,α⊥β,则m⊥α;②若m∥α,m⊥β,则α⊥β;③若α⊥β,α⊥γ,则β⊥γ;④若α∩γ=m,β∩γ=n,m∥n,则α∥β.上面命题中,真命题的序号是________(写出所有真命题的序号).7.在各个面都是正三角形的四面体PABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论中成立的是________(填序号).①BC∥平面PDF;②DF⊥平面PAE;③平面PDF⊥平面ABC;④平面PAE⊥平面ABC.8.如图所示,PA⊥平面ABCD,四边形ABCD为矩形,那么以P、A、B、C、D五个点中的三点为顶点的直角三角形的个数是________.9.如图所示,矩形ABCD中,AB=1,BC=2,PA⊥平面ABCD,且PA=1,则在BC上存在________个点使PQ⊥QD.110.称四个面均为直角三角形的三棱锥为“四直角三棱锥”,若在四直角三棱锥SABC中,∠SAB=∠SAC=∠SBC=90°,则第四个面中的直角为________.11.在正方体ABCDA1B1C1D1中,点P在侧面BB1C1C上运动,并且保持AP⊥BD1,则动点P的轨迹是________.12.如图所示,四棱锥PABCD的底面ABCD是边长为1的正方形,侧棱PA=1,PB=PD=,则它的5个面中,互相垂直的面有________对.13.如图,在四棱锥PABCD中,PA⊥底面ABCD,底面各边都相等,M是PC上的一动点,当点M满足________时,平面MBD⊥平面PCD.14.如图,棱柱ABCA1B1C1的侧面BCC1B1是菱形,B1C⊥A1B.求证:平面AB1C⊥平面A1BC1.215.如图,AB为圆O的直径,点E在圆O上,矩形ABCD所在的平面和圆O所在的平面互相垂直.求证:AE⊥平面CBE.16.如图,在四棱锥PABCD中,PD⊥平面ABCD,AD=CD,DB平分∠ADC,E为PC的中点.(1)证明:PA∥平面BDE;(2)证明:平面PAC⊥平面PDB.17.如图,在正方体ABCDA1B1C1D1中.(1)求证:平面BC1D⊥平面A1ACC1;(2)求二面角C1BDC的正切值.【参考答案与解析】31.【答案】必要不充分【解析】由直线与平面垂直的定义知为必要不充分条件.2.【答案】①③④【解析】据面面垂直的判定定理可知②正确,所以填①③④.3.【答案】②【解析】根据线面垂直的判定定理知①错;根据线面垂直的性质知②正确;③中l可能与m异面;④中l可能与m异面,也可能相交.4.【答案】④【解析】由面面垂直的判定定理可知④正确.5.【答案】④【解析】由面面垂直的定义、判定定理可得.6.【答案】②【解析】①中m与不一定垂直;③中可以得到和γ相交或∥γ;④中可以得到∥或,相交;只有②正确.7.【答案】①②④【解析】作出图形易知①正确;由BC⊥AE,BC⊥PE,可得BC⊥平面PAE,从而得DF⊥平面PAE,②正确;因为BC⊥平面PAE,BC⊂平面ABC,则平面PAE⊥平面ABC,④正确.8.【答案】9【解析】分三类:(1)在底面ABCD中,共有4个直角,因而有4个直角三角形;(2)四个侧面都是直角三角形;(3)过两条侧棱的截面中,△PAC为直角三角形.故共有9个直角三角形.9.【答案】1【解析】因为PA⊥平面ABCD,又QD⊂平面ABCD,则PA⊥QD,又PQ⊥Q...