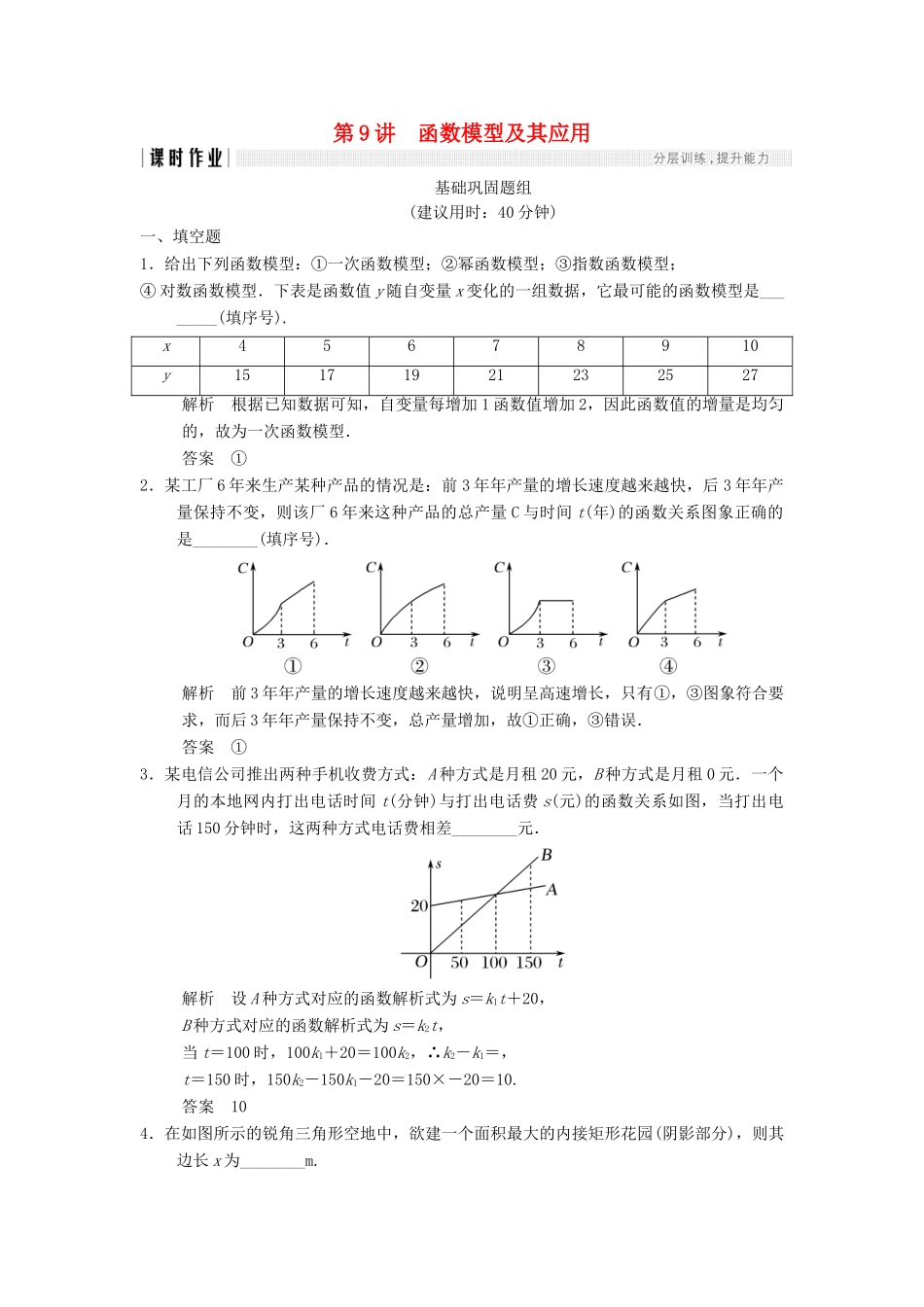
第9讲函数模型及其应用基础巩固题组(建议用时:40分钟)一、填空题1.给出下列函数模型:①一次函数模型;②幂函数模型;③指数函数模型;④对数函数模型.下表是函数值y随自变量x变化的一组数据,它最可能的函数模型是________(填序号).x45678910y15171921232527解析根据已知数据可知,自变量每增加1函数值增加2,因此函数值的增量是均匀的,故为一次函数模型.答案①2.某工厂6年来生产某种产品的情况是:前3年年产量的增长速度越来越快,后3年年产量保持不变,则该厂6年来这种产品的总产量C与时间t(年)的函数关系图象正确的是________(填序号).解析前3年年产量的增长速度越来越快,说明呈高速增长,只有①,③图象符合要求,而后3年年产量保持不变,总产量增加,故①正确,③错误.答案①3.某电信公司推出两种手机收费方式:A种方式是月租20元,B种方式是月租0元.一个月的本地网内打出电话时间t(分钟)与打出电话费s(元)的函数关系如图,当打出电话150分钟时,这两种方式电话费相差________元.解析设A种方式对应的函数解析式为s=k1t+20,B种方式对应的函数解析式为s=k2t,当t=100时,100k1+20=100k2,∴k2-k1=,t=150时,150k2-150k1-20=150×-20=10.答案104.在如图所示的锐角三角形空地中,欲建一个面积最大的内接矩形花园(阴影部分),则其边长x为________m.解析设内接矩形另一边长为y,则由相似三角形性质可得=,解得y=40-x,所以面积S=x(40-x)=-x2+40x=-(x-20)2+400(0<x<40),当x=20时,Smax=400.答案205.(2017·长春模拟)一个容器装有细沙acm3,细沙从容器底下一个细微的小孔慢慢地匀速漏出,tmin后剩余的细沙量为y=ae-bt(cm3),经过8min后发现容器内还有一半的沙子,则再经过________min,容器中的沙子只有开始时的八分之一.解析当t=0时,y=a,当t=8时,y=ae-8b=a,∴e-8b=,容器中的沙子只有开始时的八分之一时,即y=ae-bt=a,e-bt==(e-8b)3=e-24b,则t=24,所以再经过16min.答案166.A,B两只船分别从在东西方向上相距145km的甲乙两地开出.A从甲地自东向西行驶.B从乙地自北向南行驶,A的速度是40kmh,B的速度是16kmh,经过________h,AB间的距离最短.解析设经过xh,A,B相距为ykm,则y==(0≤x≤),求得函数的最小值时x的值为.答案7.某企业投入100万元购入一套设备,该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元.为使该设备年平均费用最低,该企业需要更新设备的年数为________.解析设该企业需要更新设备的年数为x,设备年平均费用为y,则x年后的设备维护费用为2+4+…+2x=x(x+1),所以x年的平均费用为y==x++1.5,由基本不等式得y=x++1.5≥2+1.5=21.5,当且仅当x=,即x=10时取等号.答案108.(2016·四川卷改编)某公司为激励创新,计划逐年加大研发奖金投入.若该公司2015年全年投入研发奖金130万元.在此基础上,每年投入的研发奖金比上一年增长12%,则该公司全年投入的研发奖金开始超过200万元的年份是________(参考数据:lg1.12=0.05,lg1.3=0.11,lg2=0.30).解析设第x年的研发奖金为200万元,则由题意可得130×(1+12%)x=200,∴1.12x=,∴x=log1.12=log1.1220-log1.1213=-===3.8.即3年后不到200万元,第4年超过200万元,即2019年超过200万元.答案2019二、解答题9.(2016·江苏卷)现需要设计一个仓库,它由上下两部分组成,上部分的形状是正四棱锥P-A1B1C1D1,下部分的形状是正四棱柱ABCD-A1B1C1D1(如图所示),并要求正四棱柱的高OO1是正四棱锥的高PO1的4倍.(1)若AB=6m,PO1=2m,则仓库的容积是多少?(2)若正四棱锥的侧棱长为6m,则当PO1为多少时,仓库的容积最大?解(1)V=×62×2+62×2×4=312(m3).(2)设PO1=x,则O1B1=,B1C1=·,∴SA1B1C1D1=2(62-x2),又由题意可得下面正四棱柱的高为4x.则仓库容积V=x·2(62-x2)+2(62-x2)·4x=x(36-x2).由V′=0得x=2或x=-2(舍去).由实际意义知V在x=2(m)时取到最大值,故当PO1=2m时,仓库容积最大....