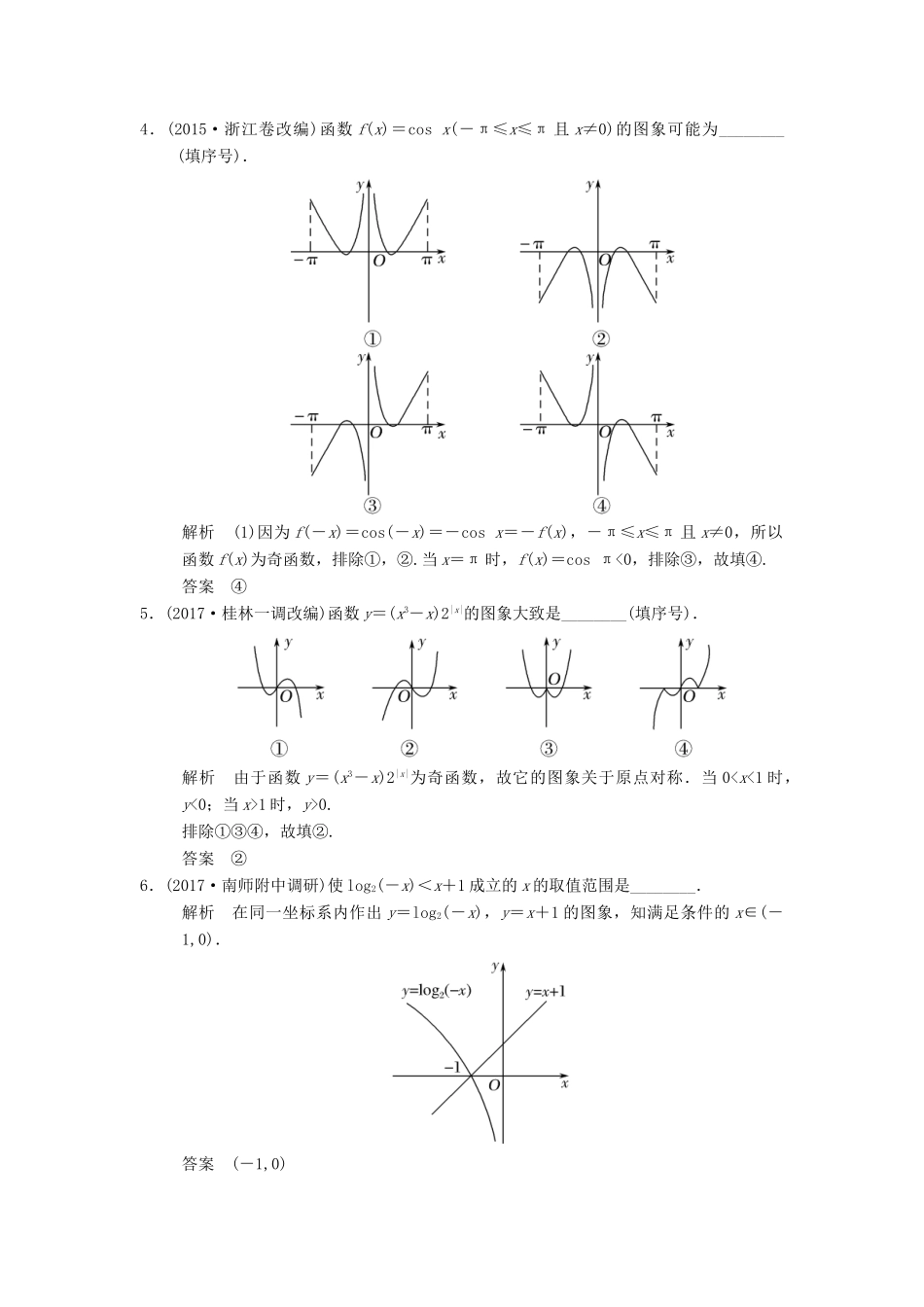
第7讲函数的图象基础巩固题组(建议用时:40分钟)一、填空题1.(2017·扬州一检)把函数y=(x-2)2+2的图象向左平移1个单位,再向上平移1个单位,所得图象对应的函数解析式是________.解析把函数y=f(x)的图象向左平移1个单位,即把其中x换成x+1,于是得y=[(x+1)-2]2+2=(x-1)2+2,再向上平移1个单位,即得到y=(x-1)2+2+1=(x-1)2+3.答案y=(x-1)2+32.小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间后,为了赶时间加快速度行驶,与以上事件吻合得最好的图象是________(填序号).解析小明匀速运动时,所得图象为一条直线,且距离学校越来越近,排除①.因交通堵塞停留了一段时间,与学校的距离不变,排除④.后来为了赶时间加快速度行驶,排除②.故填③.答案③3.已知函数f(x)的图象如图所示,则函数g(x)=logf(x)的定义域是________.解析当f(x)>0时,函数g(x)=logf(x)有意义,由函数f(x)的图象知满足f(x)>0的x∈(2,8].答案(2,8]4.(2015·浙江卷改编)函数f(x)=cosx(-π≤x≤π且x≠0)的图象可能为________(填序号).解析(1)因为f(-x)=cos(-x)=-cosx=-f(x),-π≤x≤π且x≠0,所以函数f(x)为奇函数,排除①,②.当x=π时,f(x)=cosπ<0,排除③,故填④.答案④5.(2017·桂林一调改编)函数y=(x3-x)2|x|的图象大致是________(填序号).解析由于函数y=(x3-x)2|x|为奇函数,故它的图象关于原点对称.当01时,y>0.排除①③④,故填②.答案②6.(2017·南师附中调研)使log2(-x)<x+1成立的x的取值范围是________.解析在同一坐标系内作出y=log2(-x),y=x+1的图象,知满足条件的x∈(-1,0).答案(-1,0)7.如图,定义在[-1,+∞)上的函数f(x)的图象由一条线段及抛物线的一部分组成,则f(x)的解析式为________.解析当-1≤x≤0时,设解析式为y=kx+b(k≠0).则得∴y=x+1.当x>0时,设解析式为y=a(x-2)2-1(a≠0). 图象过点(4,0),∴0=a(4-2)2-1,得a=.答案f(x)=8.设函数f(x)=|x+a|,g(x)=x-1,对于任意的x∈R,不等式f(x)≥g(x)恒成立,则实数a的取值范围是________.解析如图作出函数f(x)=|x+a|与g(x)=x-1的图象,观察图象可知:当且仅当-a≤1,即a≥-1时,不等式f(x)≥g(x)恒成立,因此a的取值范围是[-1,+∞).答案[-1,+∞)二、解答题9.已知函数f(x)=(1)在如图所示给定的直角坐标系内画出f(x)的图象;(2)写出f(x)的单调递增区间;(3)由图象指出当x取什么值时f(x)有最值.解(1)函数f(x)的图象如图所示.(2)由图象可知,函数f(x)的单调递增区间为[-1,0],[2,5].(3)由图象知当x=2时,f(x)min=f(2)=-1,当x=0时,f(x)max=f(0)=3.10.已知f(x)=|x2-4x+3|.(1)作出函数f(x)的图象;(2)求函数f(x)的单调区间,并指出其单调性;(3)求集合M={m|使方程f(x)=m有四个不相等的实根}.解(1)当x2-4x+3≥0时,x≤1或x≥3,∴f(x)=∴f(x)的图象为:(2)由函数的图象可知f(x)的单调区间是(-∞,1],(2,3),(1,2],[3,+∞),其中(-∞,1],(2,3)是减区间;(1,2],[3,+∞)是增区间.(3)由f(x)的图象知,当00且b≠1)的图象如图所示,那么函数y=logb(x-a)的图象可能是________(填序号).解析由题图可得a>1,且最小正周期T=<π,所以b>2,则y=logb(x-a)是增函数,排除①和②;当x=2时,y=logb(2-a)<0,排除④,故填③.答案③12.(2015·安徽卷改编)函数f(x)=的图象如图所示,则下列结论:①a>0,b>0,c<0;②a<0,b>0,c>0;③a<0,b>0,c<0;④a<0,b<0,c<0.其中正确的是________(填序号).解析函数定义域为{x|x≠-c},结合图象知-c>0,∴c<0.令x=0,得f(0)=,又由图象知f(0)>0,∴b>0.令f(x)=0,得x=-,结合图象知->0,∴a<0.答案③13.(2017·常州监测)已知函数f(x)=若对任意的x∈R,都有f(x)≤|k-1|成立,则实数k的取值范围为________.解析对任意x∈R,都有f(x)≤|k-1|成立,即f(x)max≤|k-1|.因为f(x)的草图如图...