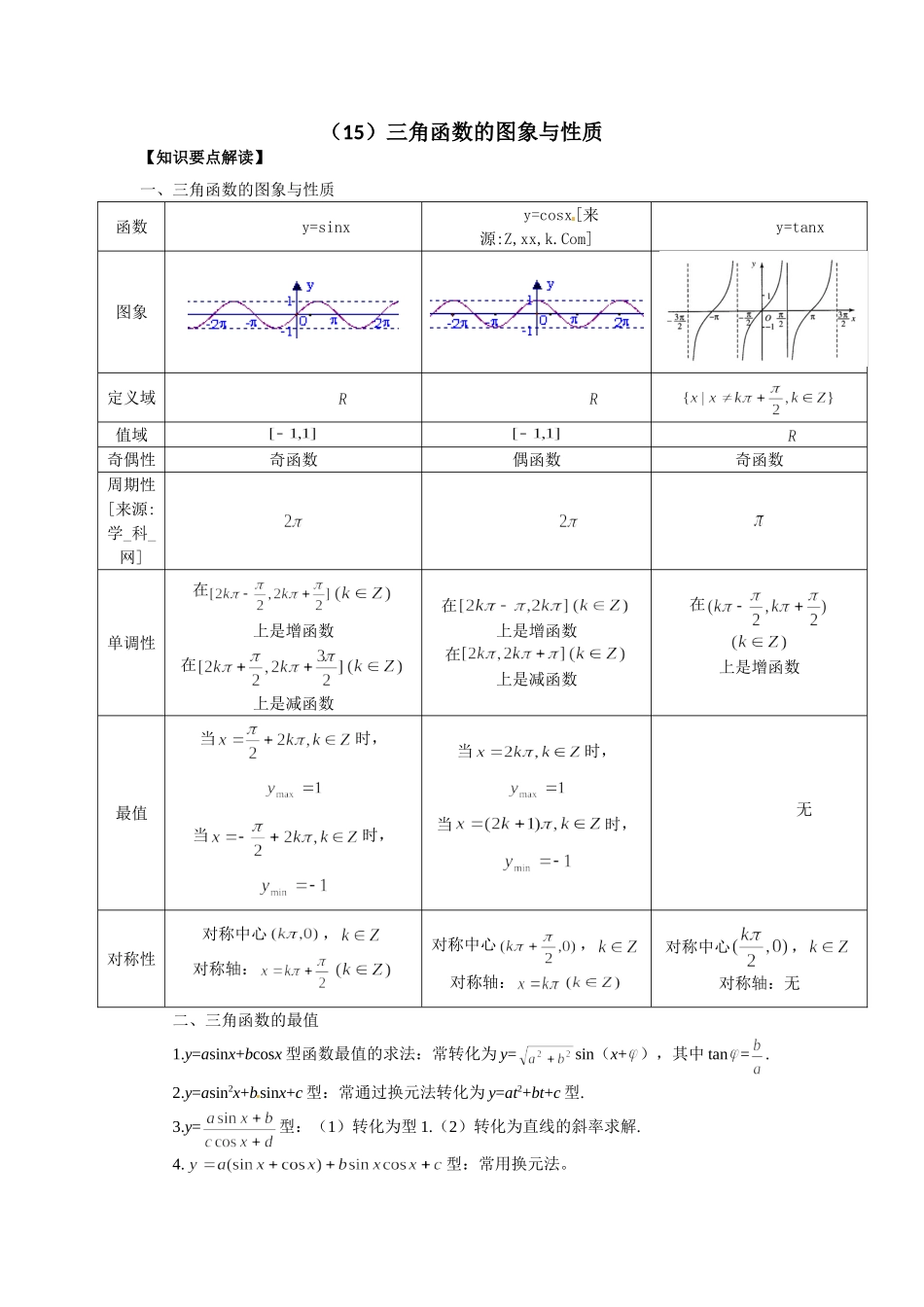
(15)三角函数的图象与性质【知识要点解读】一、三角函数的图象与性质函数y=sinxy=cosx[来源:Z,xx,k.Com]y=tanx图象定义域值域奇偶性奇函数偶函数奇函数周期性[来源:学_科_网]单调性在上是增函数在上是减函数在上是增函数在上是减函数在上是增函数最值当时,当时,当时,当时,无对称性对称中心,对称轴:对称中心,对称轴:对称中心,对称轴:无二、三角函数的最值1.y=asinx+bcosx型函数最值的求法:常转化为y=sin(x+),其中tan=.2.y=asin2x+bsinx+c型:常通过换元法转化为y=at2+bt+c型.3.y=型:(1)转化为型1.(2)转化为直线的斜率求解.4.型:常用换元法。【典型例题】例1设,,,则有(C)A.B.C.D.例2、(2007年安徽文15)函数的图象为,如下结论中正确的是_________①图象关于直线对称;②图象关于点对称;③函数在区间内是增函数;④由的图角向右平移个单位长度可以得到图象.(写出所有正确结论的编号).例3、已知,求函数的最小值。解:[来源:学&科&网Z&X&X&K]【闯关练习】1、(2007年安徽理6)函数的图象为,①图象关于直线对称;②函数在区间内是增函数;③由的图象向右平移个单位长度可以得到图象.以上三个论断中,正确论断的个数是()A.0B.1C.2D.32、(2008天津理3)设函数,,则是()A.最小正周期为的奇函数B.最小正周期为的偶函数C.最小正周期为的奇函数D.最小正周期为的偶函数3、(2007年北京文3)函数的最小正周期是()A.B.C.D.4、(2007年福建理5)已知函数的最小正周期为,则该函数的图()A.关于点对称B.关于直线对称C.关于点对称D.关于直线对称5、(2011年大纲全国卷理5)设函数,将的图像向右平移单位长度后,所得的图象与原图象重合,则的最小值等于()A.B.3C.6D.96、(2007年广东文9)已知简谐运动的图象经过点,则该简谐运动的最小正周期T和初相分别为()A.,B.,C.,D.,7、函数的一个单调增区间是()A.B.C.D.8、(2007年海南宁夏理9)若,则的值为()A.B.C.D.9、函数的最小正周期.10、函数y=sin4x+2sinxcosx-cos4x在[0,π]上的单调递增区间.是.11、函数y=|sinx|+|cosx|,x∈[0,π]的值域是.12、函数y=的最大值是_______,最小值是_______.13、(2007年四川理16)下面有五个命题:①函数y=sin4x-cos4x的最小正周期是.②终边在y轴上的角的集合是{a|a=|.③在同一坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点.[来源:学科网]④把函数⑤函数其中真命题的序号是(写出所有真命题的序号)14、已知x∈[,],函数y=cos2x-sinx+b+1的最大值为,试求其最小值.[来源:Z*xx*k.Com]15、(2010湖南)已知函数。(1)求函数的最大值;(2)求函数的零点的集合。16、(2010湖北)已知函数,.(Ⅰ)求函数的最小正周期;(Ⅱ)求函数的最大值,并求使取得最大值的的集合.[来源:学。科。网Z。X。X。K]17、求函数y=的最大值和最小值.18、求y=1+sinx+cosx+sinxcosx的值域.(15)三角函数的图象与性质【知识要点解读】一、三角函数的图象与性质函数y=sinxy=cosxy=tanx图象定义域值域奇偶性奇函数偶函数奇函数周期性单调性在上是增函数在上是减函数在上是增函数在上是减函数在上是增函数最值当时,当时,[来源:学.科.网Z.X.X.K]当时,当时,无对称性[来源:学科网]对称中心,对称轴:对称中心,对称轴:对称中心,对称轴:无二、三角函数的最值1.y=asinx+bcosx型函数最值的求法:常转化为y=sin(x+),其中tan=.2.y=asin2x+bsinx+c型:常通过换元法转化为y=at2+bt+c型.3.y=型:(1)转化为型1.(2)转化为直线的斜率求解.4.型:常用换元法。【典型例题】例1设,,,则有(C)A.B.C.D.解析:,,例2、(2007年安徽文15)函数的图象为,如下结论中正确的是①②③(写出所有正确结论的编号).①图象关于直线对称;②图象关于点对称;③函数在区间内是增函数;④由的图角向右平移个单位长度可以得到图象.例3、已知,求函数的最小值。解:,令, ∴,()∴当,即时,有最小值且最小值为。【闯关练习】1、(2007年安徽理6)函数的图象为,[来源:学&科&网Z&X&X&K]①图象关于直线对称;②...