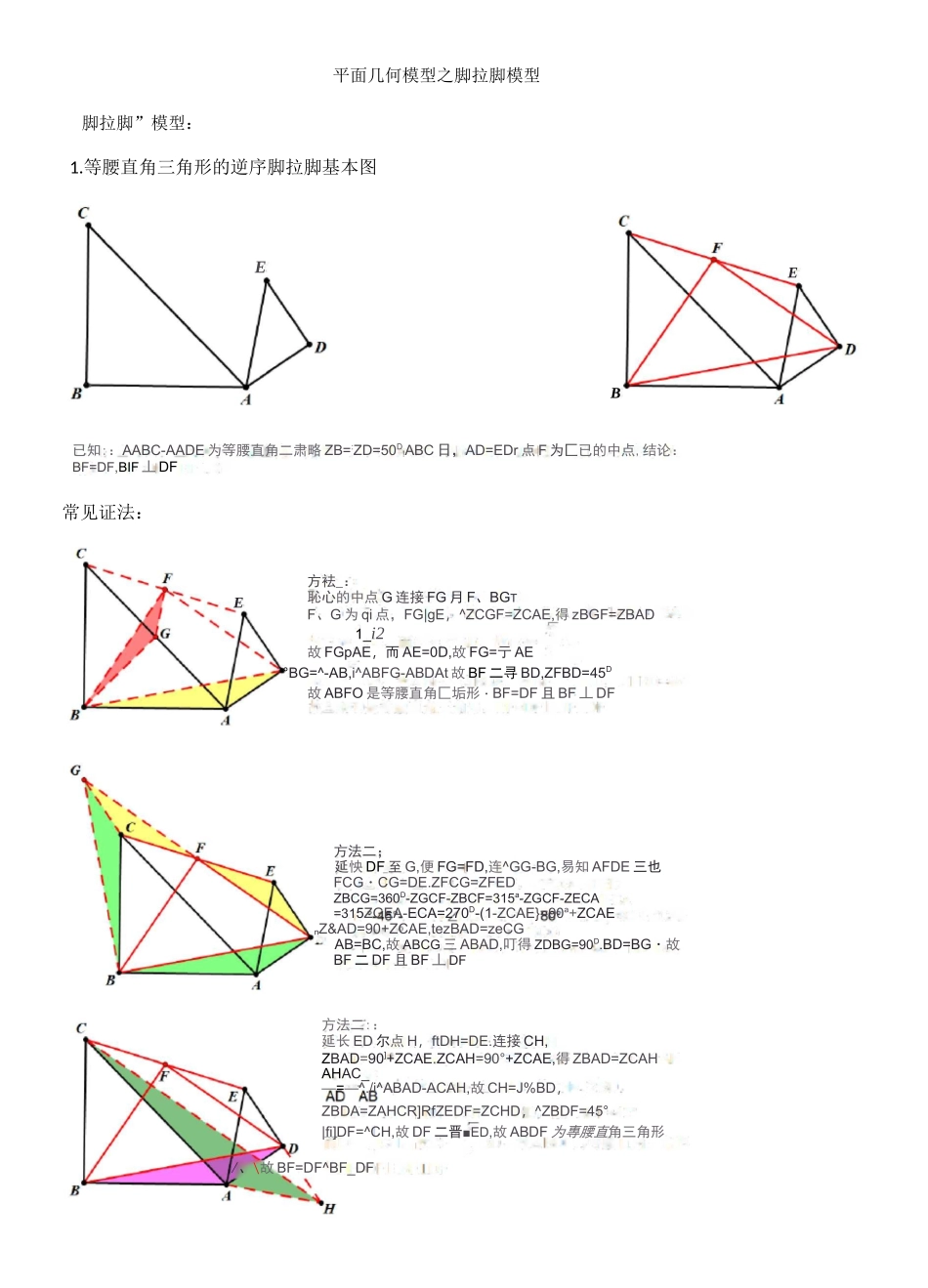
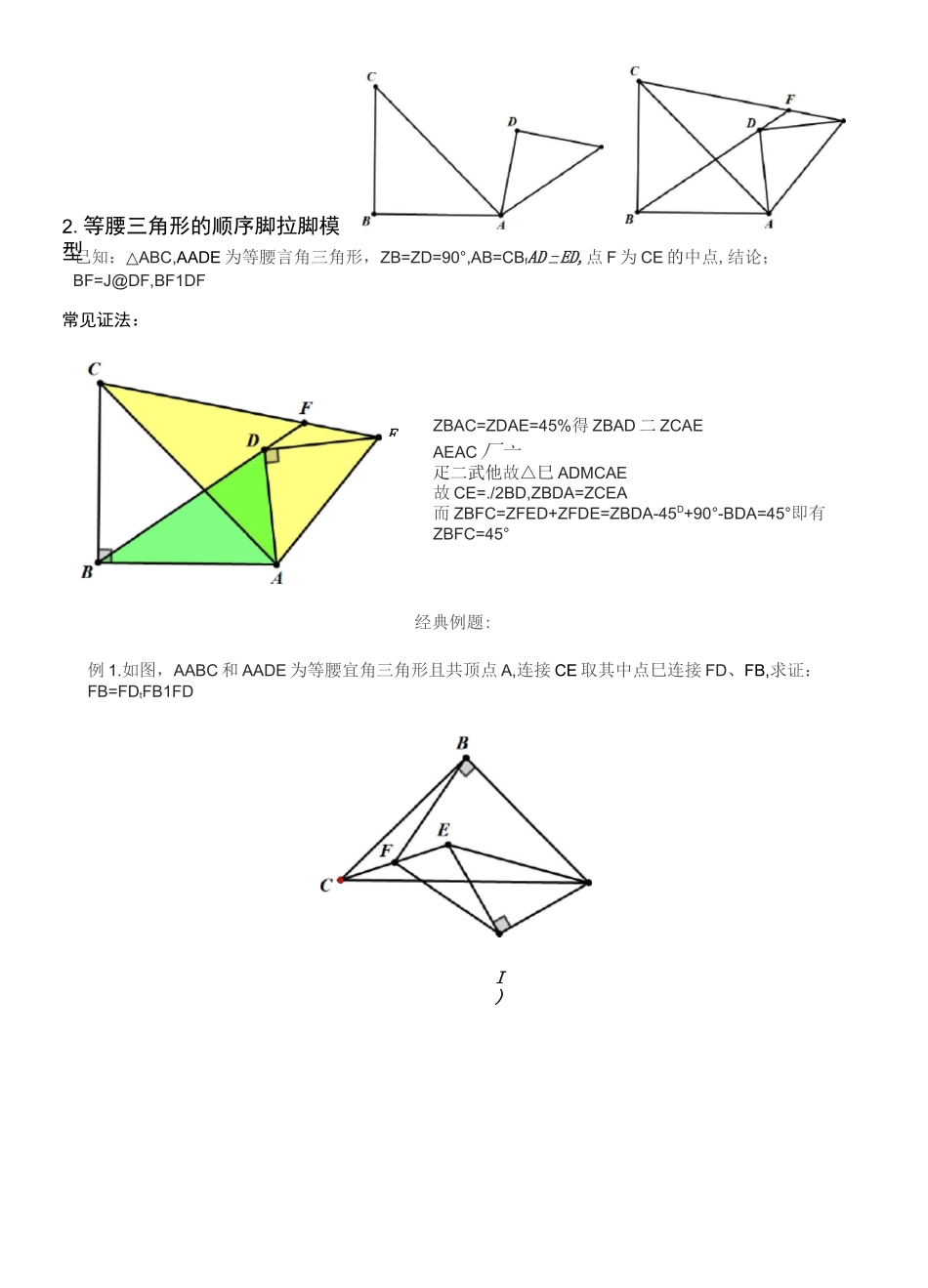
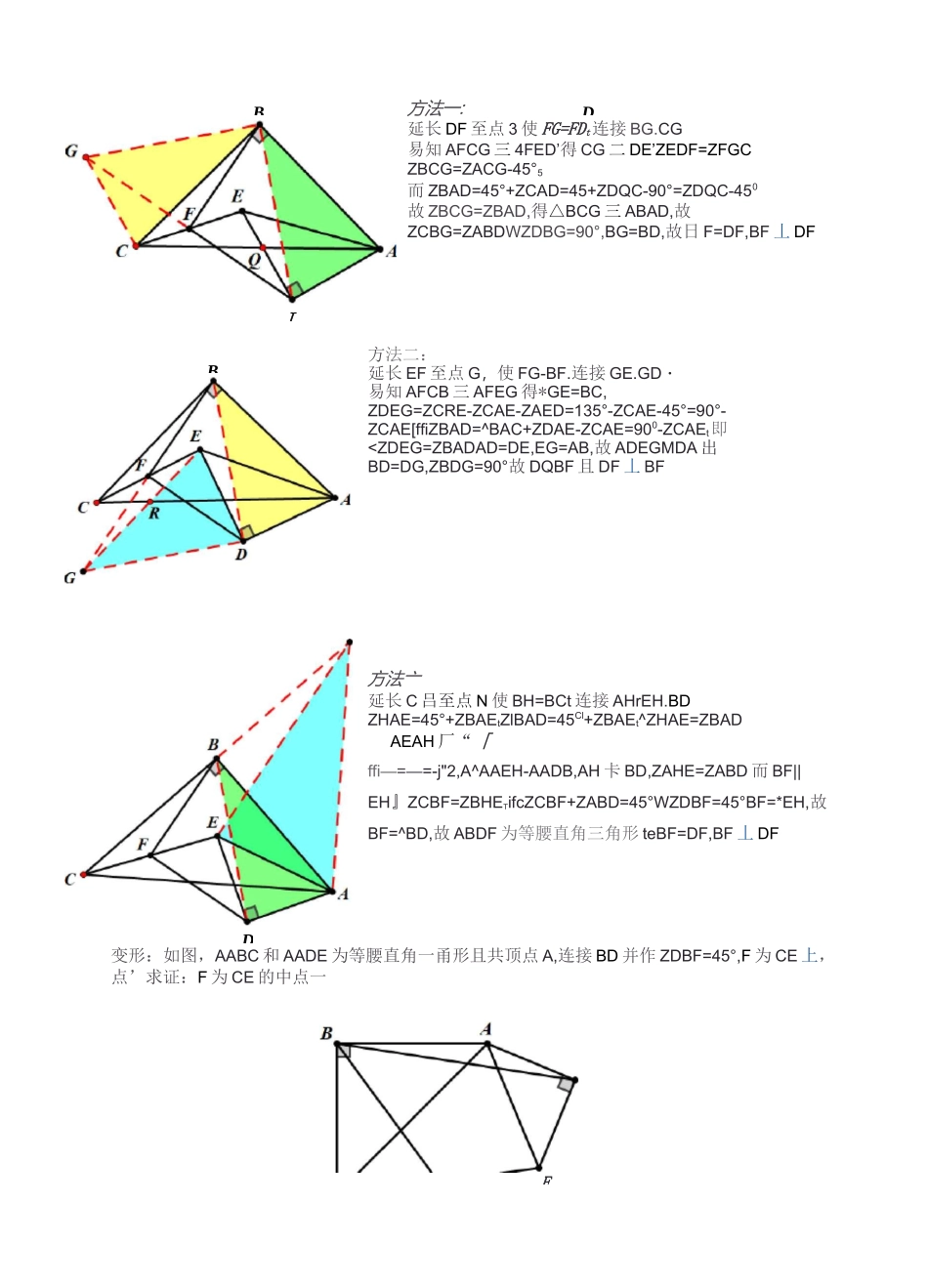
脚拉脚”模型:平面几何模型之脚拉脚模型1.等腰直角三角形的逆序脚拉脚基本图EEbB已知::AABC-AADE为等腰直角二肃略ZB=:ZD=50D!ABC日,AD=EDr点F为匚已的中点,结论:BF=DF,BIF丄DF常见证法:E方法二;延怏DF至G,便FG=FD,连^GG-BG,易知AFDE三也FCG・CG=DE.ZFCG=ZFEDZBCG=360D-ZGCF-ZBCF=315a-ZGCF-ZECA=315ZGEA-ECA=270D-(1-ZCAE}=90a+ZCAEnZ&AD=90+ZCAE,tezBAD=zeCGAB=BC,故ABCG三ABAD,叮得ZDBG=90D.BD=BG・故BF二DF且BF丄DF方袪_:恥心的中点G连接FG月F、BGTF、G为qi点,FG|gE,^ZCGF=ZCAE,得zBGF=ZBAD1_i2故FGpAE,而AE=0D,故FG=亍AE°BG=^-AB,i^ABFG-ABDAt故BF二寻BD,ZFBD=45D故ABFO是等腰直角匚垢形・BF=DF且BF丄DF方法二::延长ED尔点H,ftDH=DE.连接CH,ZBAD=90]+ZCAE.ZCAH=90°+ZCAE,得ZBAD=ZCAHAHAC_—=—^./i^ABAD-ACAH,故CH=J%BD,ZBDA=ZAHCR]RfZEDF=ZCHD,^ZBDF=45°|fi]DF=^CH,故DF二晋■ED,故ABDF为專腰直角三角形/、\故BF=DF^BF_DFI)己知:△ABC,AADE为等腰言角三角形,ZB=ZD=90°,AB=CBfAD二ED,点F为CE的中点,结论;BF=J@DF,BF1DF常见证法:ZBAC=ZDAE=45%得ZBAD二ZCAEAEAC厂亠疋二武他故△巳ADMCAE故CE=./2BD,ZBDA=ZCEA而ZBFC=ZFED+ZFDE=ZBDA-45D+90°-BDA=45°即有ZBFC=45°经典例题:例1.如图,AABC和AADE为等腰宜角三角形且共顶点A,连接CE取其中点巳连接FD、FB,求证:FB=FDtFB1FDE2.等腰三角形的顺序脚拉脚模型方法一:延长DF至点3使FG=FDt连接BG.CG易知AFCG三4FED’得CG二DE’ZEDF=ZFGCZBCG=ZACG-45°5而ZBAD=45°+ZCAD=45+ZDQC-90°=ZDQC-450故ZBCG=ZBAD,得△BCG三ABAD,故ZCBG=ZABDWZDBG=90°,BG=BD,故日F=DF,BF丄DF方法二:延长EF至点G,使FG-BF.连接GE.GD・易知AFCB三AFEG得*GE=BC,ZDEG=ZCRE-ZCAE-ZAED=135°-ZCAE-45°=90°-ZCAE[ffiZBAD=^BAC+ZDAE-ZCAE=900-ZCAEt即故ZACD=ZDEGXAC=AB.故心EG,CEDE*得AACDHAGED,故AD二DG,ZADG=90C故AADG为等腰直角一肃开纭所以AM=DIVhAK1丄DM参考答案:A