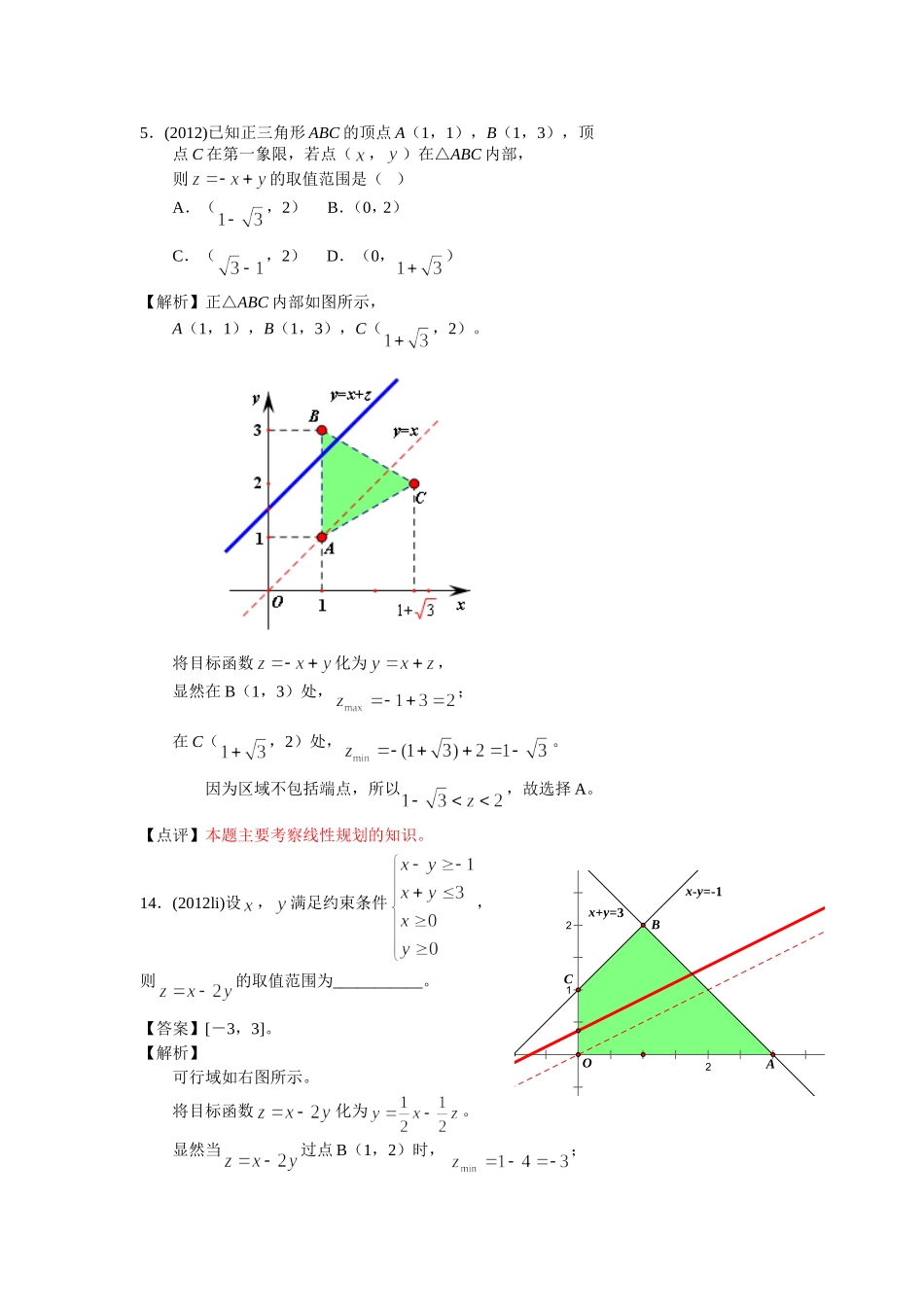
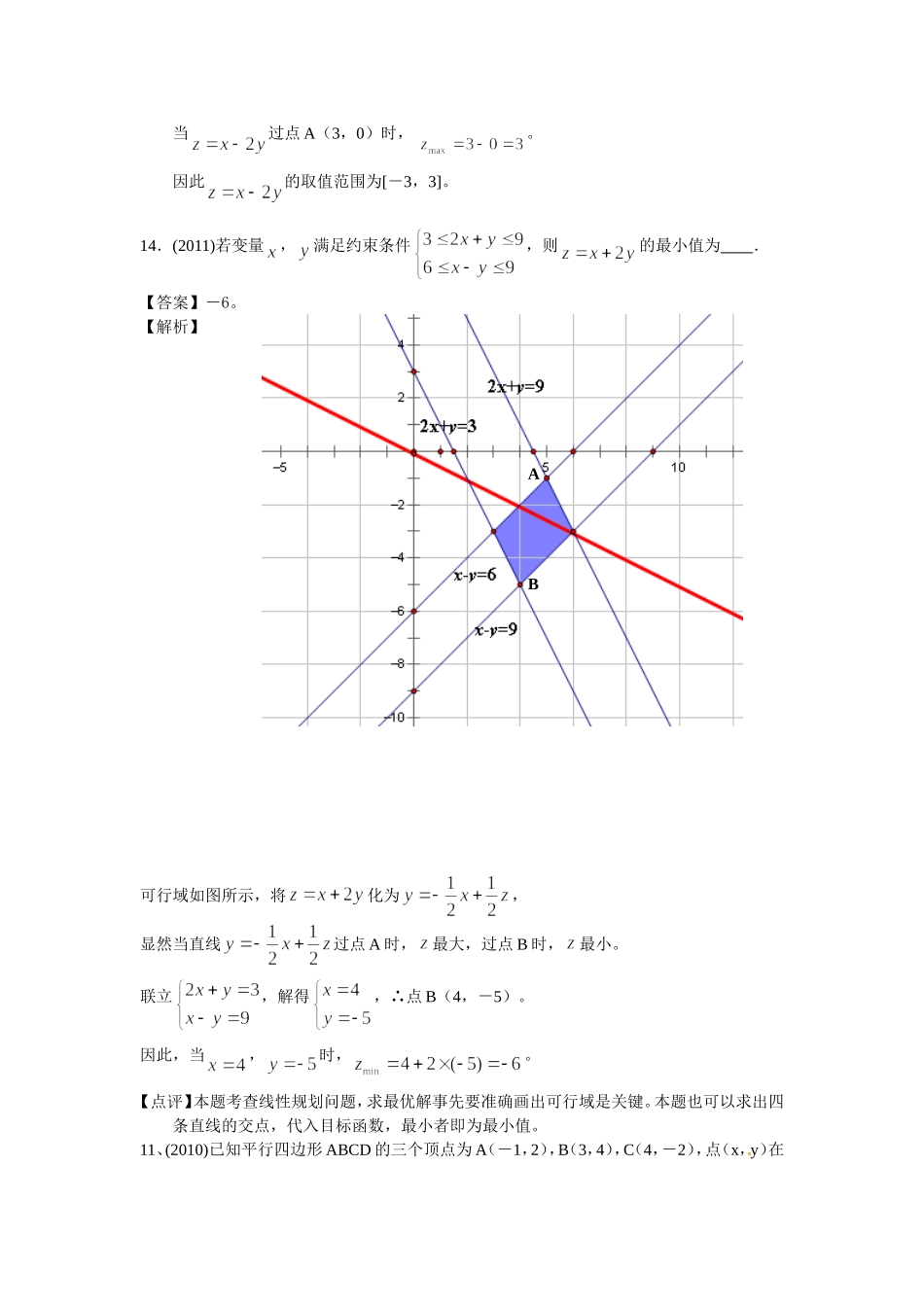
5.(2012)已知正三角形ABC的顶点A(1,1),B(1,3),顶点C在第一象限,若点(,)在△ABC内部,则的取值范围是()A.(,2)B.(0,2)C.(,2)D.(0,)【解析】正△ABC内部如图所示,A(1,1),B(1,3),C(,2)。将目标函数化为,显然在B(1,3)处,;在C(,2)处,。因为区域不包括端点,所以,故选择A。【点评】本题主要考察线性规划的知识。14.(2012li)设,满足约束条件,则的取值范围为___________。【答案】[-3,3]。【解析】可行域如右图所示。将目标函数化为。显然当过点B(1,2)时,;212x+y=3x-y=-1BACO当过点A(3,0)时,。因此的取值范围为[-3,3]。14.(2011)若变量,满足约束条件,则的最小值为.【答案】-6。【解析】可行域如图所示,将化为,显然当直线过点A时,最大,过点B时,最小。联立,解得,∴点B(4,-5)。因此,当,时,。【点评】本题考查线性规划问题,求最优解事先要准确画出可行域是关键。本题也可以求出四条直线的交点,代入目标函数,最小者即为最小值。11、(2010)已知平行四边形ABCD的三个顶点为A(-1,2),B(3,4),C(4,-2),点(x,y)在AB平行四边形ABCD的内部,则的取值范围是()A.(-14,16)B.(-14,20)C.(-12,18)D.(-12,20)【解析】选择B。先画出可行域,将化为。如图所示,当直线过点D(0,-4)时,;当直线过点B(3,4)时,。因此,的取值范围是(-14,20)6、(2009)设满足,则()A.有最小值2,最大值3B.有最小值2,无最大值C.有最大值3,无最小值D.既无最小值,也无最大值【解析】画出不等式表示的平面区域,如右图,由z=x+y,得y=-x+z,令z=0,画出y=-x的图象,当它的平行线经过A(2,0)时,z取得最小值,最小值为z=2,无最大值,故选B。11.(2012)当时,,则的取值范围是()A.(0,)B.(,1)C.(1,)D.(,2)【解析】显然要使不等式成立,必有。在同一坐标系中画出与的图象。若时,,当且仅当,,即。解得,故选择B。12.(2011)已知函数的周期为2,当[-1,1]时,,那么函数的图像与函数的图像的交点共有()A.10个B.9个C.8个D.1个【解析】利用周期性,画出在[-1,13]上的图像,函数的值域为[0,1];当时,,利用图像的对称性画出的图像。两图像如图所示,两函数图像共有10个交点,选A。【点评】本小题主要考查函数的的性质和利用周期性和对称变换作图象的方法。突出数形结合思想的应用,这是高考数学数学思想方法的具体体现。12.(2011li)函数的图像与函数()的图像所有交点的横坐标之和等于()A.2B.4C.6D.8【解析】因为函数的图像与函数的图像在区间[-2,4]上关于点(1,0)中心对称,而且两函数图像在中心的左右两边各有4个交点,且分别关于点(1,0)对称,所以,每两个对应点的横坐标的和都是2,如图所示,因此,因此所有交点的横坐标之和等于,选择D。【点评】本题综合考察函数的图象和性质,特别是对称性,方程的根(零点)。要注意对称性的把握与运用。12、(2010)已知函数,若,,互不相等,且,则的取值范围是()A.(1,10)B.(5,6)C.(10,12)D.(20,24)【解析】选择C。不妨设,由,结合图象得,,,因为,所以,,,因此=。12、(2009)用min{a,b,c}表示a,b,c三个数中的最小值。设,,}(),则的最大值为()A.4B.5C.6D.7【解析】画出y=2x,y=x+2,y=10-x的图象,如右图,观察图象可知,当0≤x≤2时,f(x)=2x,当2≤x≤3时,f(x)=x+2,当x>4时,f(x)=10-x,f(x)的最大值在x=4时取得为6,故选C。