管理运筹学排队论VIP免费

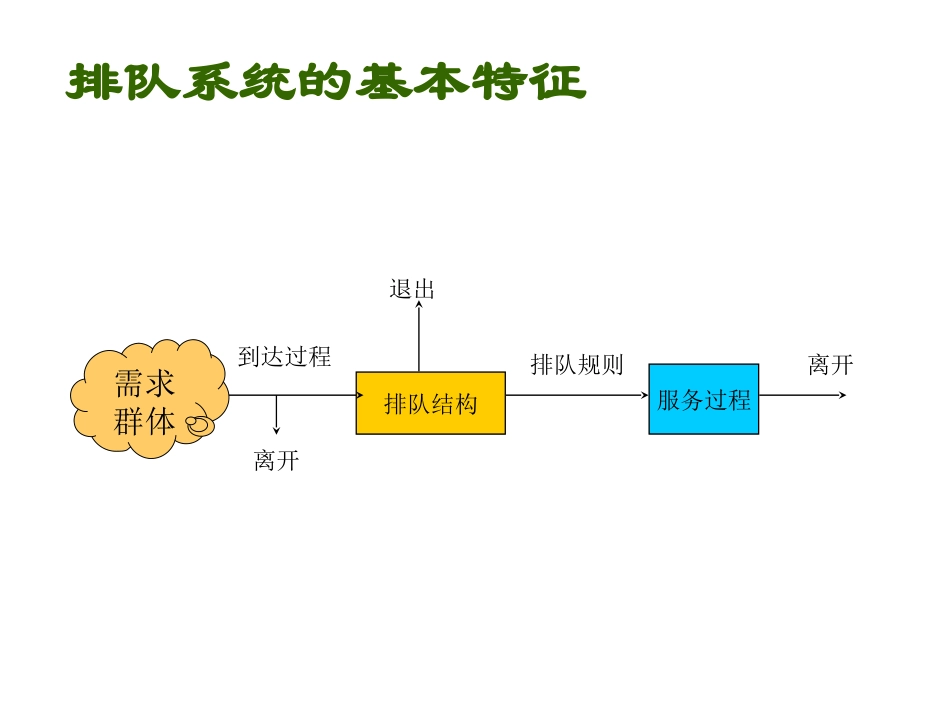
运筹学－排队论WheretheTimeGoes美国人一生中平均要花费--6年吃5年排队等待4年做家务2年回电话不成功1年寻找放置不当的物品8个月打开邮寄广告6个月停在红灯前排队系统的基本特征离开排队规则到达过程排队结构服务过程退出离开需求群体商业服务系统系统类型顾客服务台理发店人理发师银行出纳服务人出纳ATM机服务人ATM机商店收银台人收银员管道服务阻塞的管道管道工电影院售票窗口人售票员机场检票处人航空公司代理人经纪人服务人股票经纪人内部服务系统系统类型顾客服务台秘书服务雇员秘书复印服务雇员复印机计算机编程服务雇员程序员大型计算机雇员计算机急救中心雇员护士传真服务雇员传真机物料处理系统货物物料处理单元维护系统设备维修工人质检站物件质检员运输服务系统系统类型顾客服务台公路收费站汽车收费员卡车装货地卡车装货工人港口卸货区轮船卸货工人等待起飞的飞机飞机跑道航班服务人飞机出租车服务人出租车电梯服务人电梯消防部门火灾消防车停车场汽车停车空间急救车服务人急救车到达过程静态动态预约定价接受/拒绝不加入排队退出排队恒定到达率的随机到达变动到达率的随机到达由设施控制顾客控制到达过程到达过程的内容顾客总体数或顾客源数有限或无限顾客的到达类型单个或成批顾客的到达间隔时间间隔时间分布排队结构领号多条队列有限队长有限队长有限或无限队长快速通道排队结构单一队列允许或不允许移动排队结构-例多队多服务台领号34826101211579单队多服务台入口·þÎñ̨...¹Ë¿ÍÔ´ÐèÒª·þÎñ·þÎñÍê±Ï¶ÓÁÐ排队规则排队规则静态(FCFS规则)(LCFS规则).动态基于排队状况选择即与特定顾客特征选择等待的顾客数协商优先级强占顾客服务时间(SPT规则)排队规则的内容损失制系统服务台被占用时新到的顾客将离开等待制系统FCFSLCFSRSPR混合制系统损失制与等待制的混合服务过程服务过程静态服务过程动态服务过程自我服务机械速度不同的服务率开关服务通道服务过程的内容服务台数量单个或多个每次服务顾客的数量单个或成批服务顾客的时间分布时间分布常用的记号n––系统中的顾客数––平均到达率，即单位时间内平均到达的顾客数––平均服务率，即单位时间内服务完毕的顾客数Sn(t)––时刻t系统中有n个顾客Pn(t)––时刻t系统状态Sn(t)的概率C––服务台的个数M––顾客相继到达的时间间隔服从负指数分布D––顾客相继到达的时间间隔服从定长分布Ek––顾客相继到达的时间间隔服从k阶Erlang分布排队系统的符号表示一个排队系统的特征可以用六个参数表示，形式为：[A／B／C]：[d／e／f]其中A––顾客到达的概率分布，可取M、D、Ek等；B––服务时间的概率分布，可取M、D、Ek等；C––服务台个数，取正整数；d––排队系统的最大容量，可取正整数或；e––顾客源的最大容量，可取正整数或；f––排队规则，可取FCFS、LCFS等。[M/M/1]：[//FCFS]表示：顾客到达的时间间隔是负指数分布服务时间是负指数分布一个服务台排队系统和顾客源的容量都是无限实行先到先服务的一个服务系统顾客到达和服务的时间分布Poisson流（Poisson过程）定义满足以下四个条件的输入流称为Poisson流（Poisson过程）1、平稳性：在时间区间[t,t+t)内到达k个顾客的概率与t无关，只与t有关。记为pk(t）。2、无后效性：不相交的时间区间内到达的顾客数互相独立。3、普通性：设在[t,t+t）内到达多于一个顾客的概率为q(t），则q(t)=o(t)即4、有限性：任意有限个区间内到达有限个顾客的概率等于一。即0t)t(qlim0tptkk()10Poisson流与Poisson分布定理对于一个参数为的Poisson流，在[0，t]内到达k个顾客的概率为即服从以为参数的Poisson分布。pttkekkkt()()!,,0120=1=3=7Pk(1)x.4.3.2.10Poisson流与负指数分布之间的关系定理在排队系统中，如果单位时间内顾客到达数服从以为参数的Poisson分布，则顾客相继到达的时间间隔服从以为参数的负指数分布。0t00>t)(tetf=0.4/1)(tE2/1)(tVar1/为平均到达间隔时间k阶Erlang分...