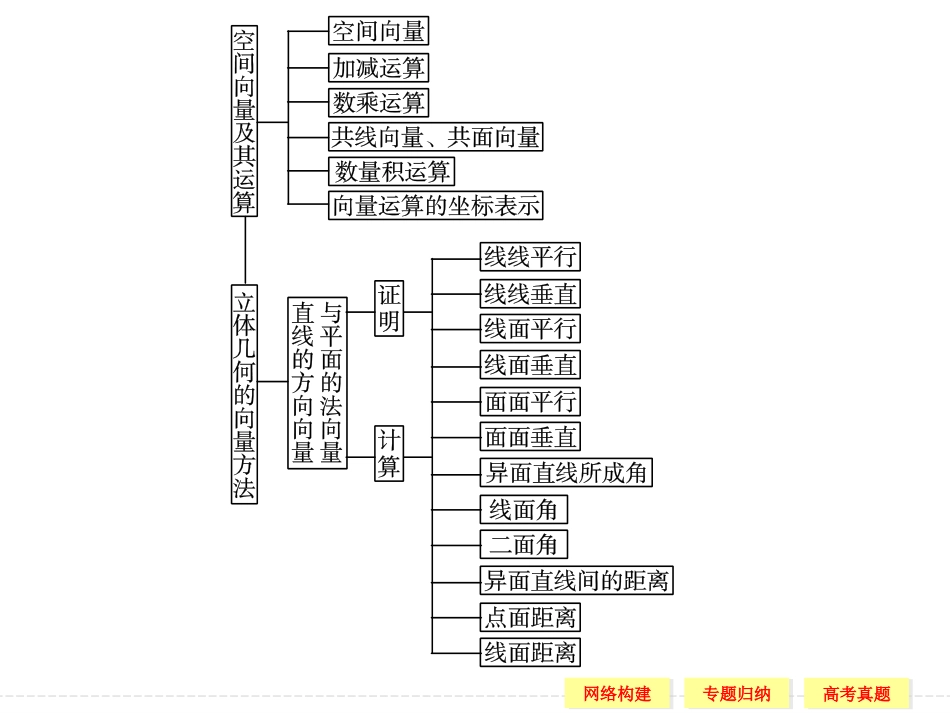
网络构建网络构建专题归纳专题归纳高考真题高考真题知识网络本章归纳整合网络构建网络构建专题归纳专题归纳高考真题高考真题网络构建网络构建专题归纳专题归纳高考真题高考真题空间向量的运算及运算律空间向量加法、减法、数乘、向量的意义及运算律与平面向量类似,空间任意两个向量都可以通过平移转化为平面向量,两个向量相加的三角形法则与平行四边形法则仍然成立.两个向量的数量积的计算向量的数量积运算要遵循数量积的性质和运算律,常用于有关向量相等、两向量垂直、射影、夹角等问题中.空间向量的坐标运算,关键是建立恰当的空间坐标系,然后再利用有关公式计算求解.常用向量的直角坐标运算来证明向量的垂直和平行问题,利用向量的夹角公式和距离公式求解空间角与空间距离的问题.要点归纳1.2.3.网络构建网络构建专题归纳专题归纳高考真题高考真题空间向量的分解定理说明:用三个不共面的已知向量{a,b,c}可以线性表示出空间任意一个向量,而且表示的结果是唯一的.利用向量解决几何问题具有快捷、有效的特征.一般方法如下:先将原问题转化为等价的向量问题,即将已知条件中的角转化为向量的夹角,线段长度转化为向量的模,并用已知向量表示出未知向量,然后利用向量的运算解决该向量问题,从而原问题得解.利用向量坐标解决立体几何问题的关键在于找准位置,建立适当、正确的空间坐标系,难点是在已建好的坐标系中表示出已知点的坐标,只有正确表示出已知点的坐标,才能通过向量的坐标运算,实现几何问题的代数化解法.4.5.6.网络构建网络构建专题归纳专题归纳高考真题高考真题专题一空间向量及其运算空间向量及其运算的知识与方法与平面向量及其运算类似,是平面向量的拓展,主要考查空间向量的共线与共面以及数量积运算,是用向量法求解立体几何问题的基础.网络构建网络构建专题归纳专题归纳高考真题高考真题则f1=a,f2=2b,f3=3c,则f=f1+f2+f3=a+2b+3c,∴|f|2=(a+2b+3c)(a+2b+3c)=|a|2+4|b|2+9|c|2+4a·b+6a·c+12b·c=14+4cos60°+6cos60°+12cos60°=14+2+3+6=25,∴|f|=5,即所求合力的大小为5.【例1】沿着正四面体O-ABC的三条棱OA→、OB→、OC→的方向有大小等于1、2和3的三个力f1,f2,f3.试求此三个力的合力f的大小以及此合力与三条棱所夹角的余弦值.解如图所示,用a,b,c分别代表棱OA→、OB→、OC→上的三个单位向量,网络构建网络构建专题归纳专题归纳高考真题高考真题且cos〈f,a〉=f·a|f|·|a|=|a|2+2a·b+3a·c5=1+1+325=710,同理可得:cos〈f,b〉=45,cos〈f,c〉=910.网络构建网络构建专题归纳专题归纳高考真题高考真题向量作为工具来研究几何,真正使几何中的形与代数中的数实现了有机的结合,给立体几体的研究带来了极大的便利,不论证明平行还是垂直,只需简单的运算就可解决问题.专题二空间向量与空间位置关系网络构建网络构建专题归纳专题归纳高考真题高考真题【例2】已知正方体ABCD-A1B1C1D1中,E、F分别在DB、D1C上,且DE=D1F=23a,其中a为正方体棱长.求证:EF∥平面BB1C1C.证明如图,建立空间直角坐标系D-xyz,则E(a3,a3,0),F(0,a3,2a3),故EF→=(-a3,0,2a3).又AB→=(0,a,0),显然为平面BB1C1C的一个法向量,网络构建网络构建专题归纳专题归纳高考真题高考真题而AB→·EF→=(0,a,0)·(-a3,0,2a3)=0,∴AB→⊥EF→.又E∉平面BB1C1C,因此EF∥平面BB1C1C.网络构建网络构建专题归纳专题归纳高考真题高考真题在棱长为1的正方体ABCD-A1B1C1D1中,E为棱BC的中点,点F是棱CD上的动点,试确定点F的位置,使得D1E⊥平面AB1F.【例3】解如图建立空间直角坐标系:则A(1,0,0),B1(1,1,1),D1(0,0,1),E(12,1,0).设F(0,y,0),则AB1→=(0,1,1),AF→=(-1,y,0),D1E→=(12,1,-1),网络构建网络构建专题归纳专题归纳高考真题高考真题要使D1E⊥平面AB1F,只需D1E→·AB1→=0,D1E→·AF→=0,即1-1=0,-12+y=0,即y=12.∴当F为CD中点时,有D1E⊥平面AB1F.网络构建网络构建专题归纳专题归纳高考真题高考真题正方体ABCD-...