八年级-正方形VIP免费

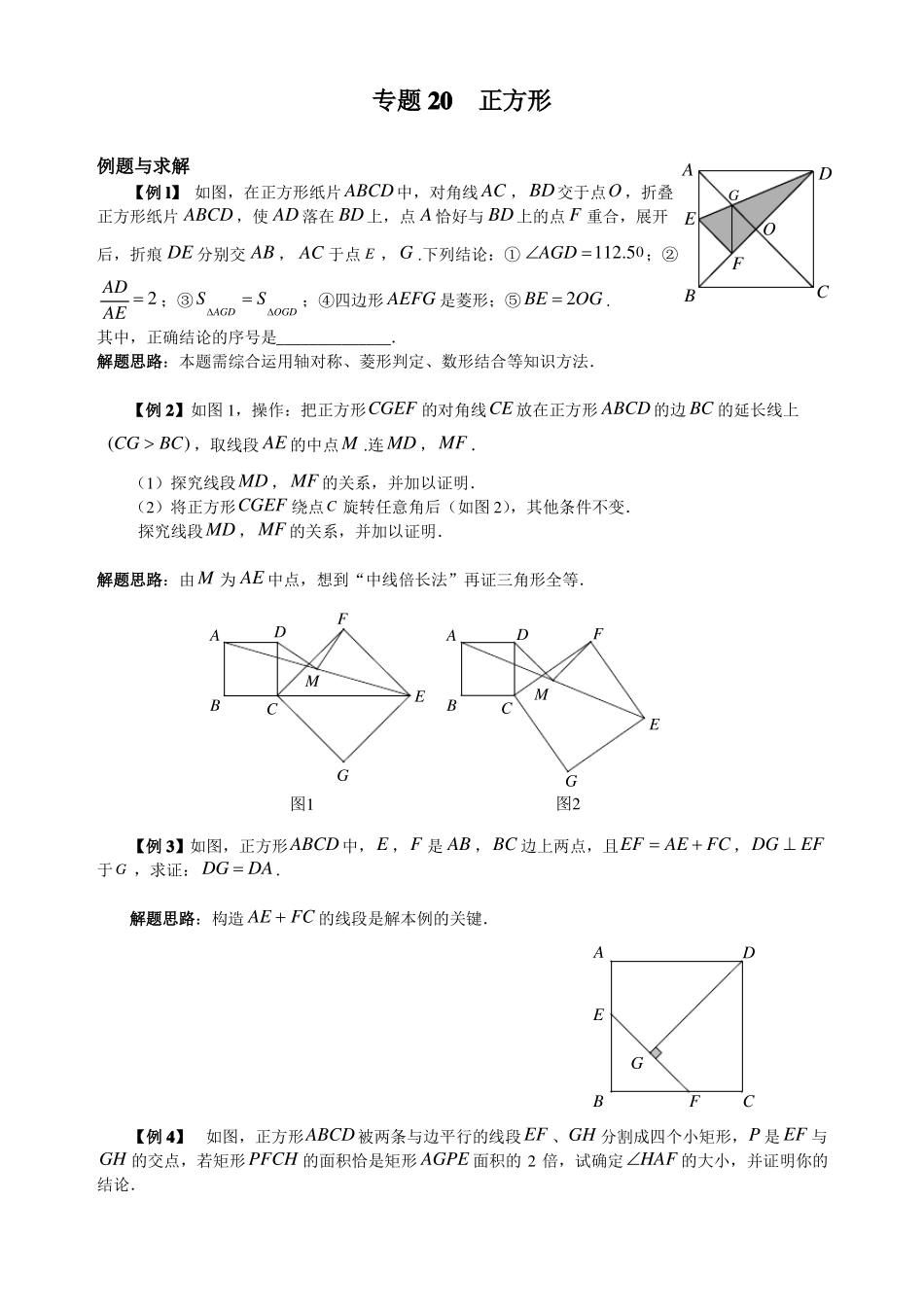
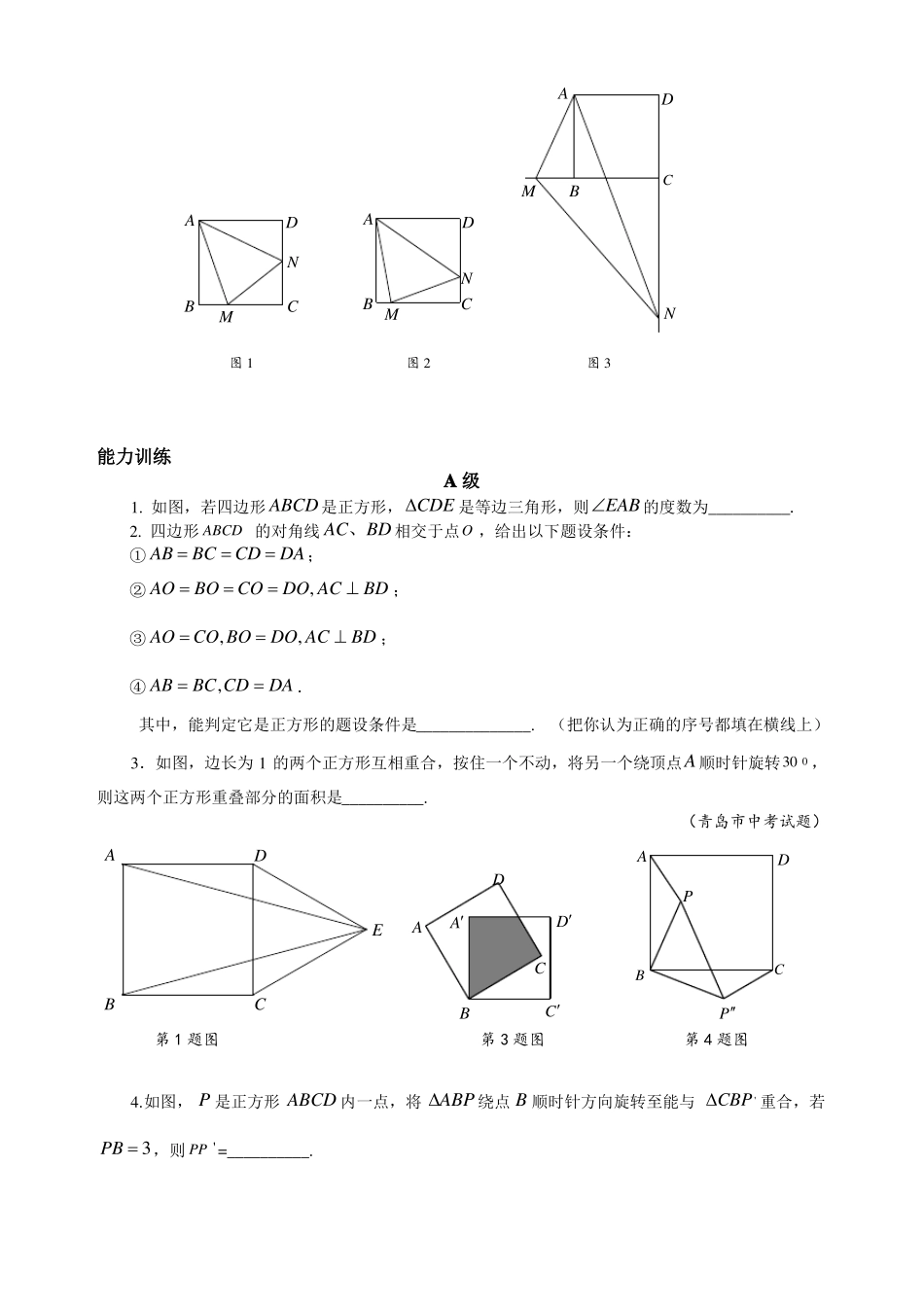
专题20正方形例题与求解AG【例l】如图，在正方形纸片ABCD中，对角线AC，BD交于点O，折叠正方形纸片ABCD，使AD落在BD上，点A恰好与BD上的点F重合，展开E后，折痕DE分别交AB，AC于点E，G.下列结论：①AGD112.5；②0DOFBCAD2；③SAGDSOGD；④四边形AEFG是菱形；⑤BE2OG.AE其中，正确结论的序号是______________．解题思路：本题需综合运用轴对称、菱形判定、数形结合等知识方法．【例2】如图1，操作：把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上(CGBC)，取线段AE的中点M.连MD，MF．（1）探究线段MD，MF的关系，并加以证明．（2）将正方形CGEF绕点C旋转任意角后（如图2），其他条件不变．探究线段MD，MF的关系，并加以证明．解题思路：由M为AE中点，想到“中线倍长法”再证三角形全等．ADMFADFBCEBCMEG图2G图1【例3】如图，正方形ABCD中，E，F是AB，BC边上两点，且EFAEFC，DGEF于G，求证：DGDA.解题思路：构造AEFC的线段是解本例的关键．ADEG【例4】如图，正方形ABCD被两条与边平行的线段EF、GH分割成四个小矩形，P是EF与GH的交点，若矩形PFCH的面积恰是矩形AGPE面积的2倍，试确定HAF的大小，并证明你的结论．BFC解题思路：先猜测HAF的大小，再作出证明，解题的关键是由条件及图形推出隐含的线段间的关系．AGEPDHF【例5】如图，在正方形ABCD中，E，F分别是边BC，CD上的点，满足EFBEDF，BCAE,AF分别与对角线BD交于点M,N．求证：（1）EAF45；（2）MNBMDN．解题思路：对于（1），可作辅助线，创造条件，再通过三角形全等，即可解答；对于（2），很容易联想到直角三角形三边关系．2220ANDFMBEC0【例6】已知：正方形ABCD中，MAN45，MAN绕点A顺时针旋转，它的两边分别交CB，DC（或它们的延长线）于点M,N．当MAN绕点A旋转到BMDN时（如图1），易证BMDNMN．（1）当MAN绕点A旋转到BMDN时（如图2），线段BM,DN和MN之间有怎样的数量关系？写出猜想，并加以证明；（2）当MAN绕点A旋转到如图3的位置时，线段BM,DN和MN之间又有怎样的数量关系？请直接写出你的猜想．解题思路：对于（2），构造DNBM是解题的关键．ADMADNBCADNBM图1CBM图2C图3N能力训练A级1.如图，若四边形ABCD是正方形，CDE是等边三角形，则EAB的度数为__________.2.四边形ABCD的对角线AC、BD相交于点O，给出以下题设条件：①ABBCCDDA；②AOBOCODO,ACBD；③AOCO,BODO,ACBD；④ABBC,CDDA．其中，能判定它是正方形的题设条件是______________.（把你认为正确的序号都填在横线上）3．如图，边长为1的两个正方形互相重合，按住一个不动，将另一个绕顶点A顺时针旋转30，则这两个正方形重叠部分的面积是__________.（青岛市中考试题）0ADDAPDEAACDBCCPB第1题图第3题图第4题图BC4.如图，P是正方形ABCD内一点，将ABP绕点B顺时针方向旋转至能与CBP重合，若'PB3，则PP'=__________.5.将n个边长都为1cm的正方形按如图所示摆放，点A1,A2,An分别是正方形的中心，则n个正方形重叠形成的重叠部分的面积和为()A.12nn121cmB．cm2C.cmD.()ncm24444BCA2A1A3A4A5AO第5题图第6题图FE6.如图，以RtBCA的斜边BC为一边在BCA的同侧作正方形BCEF，设正方形的中心为O，连接AO，如果AB4,AO62，则AC的长为()A.12B．8C.43D.827．如图，正方形ABCD中，CEMN,MCE35，那么ANM是()A.45B．55C.65D.758．如图，正方形ABCD的面积为256，点F在AD上，点E在AB的延长线上，RtCEF的面积为200，则BE的值是()A．15B．12C．11D．1000000ANDDFCEBMCABE第8题图第7题图9．如图，在正方形ABCD中，E是AD边的中点，BD与CE交于F点，求证：AFBE．AEFDBC10.（1）如图1，已知正方形ABCD和正方形CGEF(CGBC)，B,C,G在同一条直线上，M为线段AE的中点．探究：线段MD,MF的关系．（2）如图2，若将正方形CGEF绕点C顺时针旋转45，使得正方形CGEF的对角线CE在正方形ABCD的边BC的延长线上，M为AE的中点．试问：（1）中探究的结论是否成立？若成立，请证明；若不成立，请说明理由．AFADE0DFMBCMEBCGG图1图2B级1.如图，在四边形ABCD中，ADDC,ADCABC...