传热学-第二章_稳态导热_幻灯片VIP免费

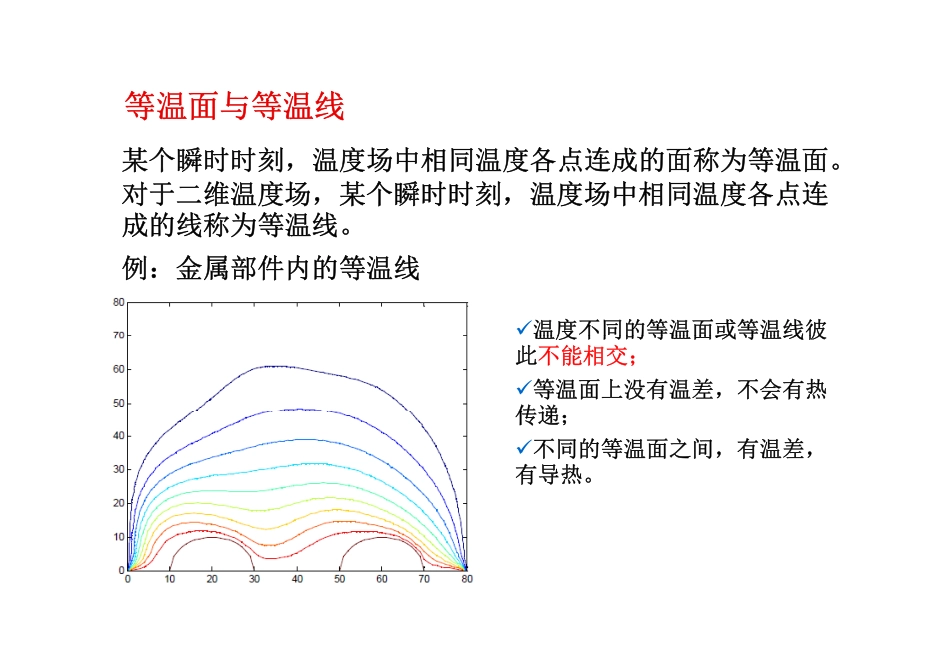
第章态热第二章稳态热传导本章着重讨论稳态导热问题。首先引出导热基本定律的最一般的数学表达式，然后介绍导热微分方程及相应的初始与边界条件，他们构成了导热问题的完整的数学描写。在此基础上针对几个典型的维导热问题（平板圆柱矩形基础上，针对几个典型的一维导热问题（平板、圆柱、矩形肋片）进行分析求解，以获得物体中的温度分布和热流量的计算式。计算式。§21导热基本定律§2-1导热基本定律一几个基本概念、几个基本概念温度场：不同时刻空间所有各点温度分布的总称温度场是时间和空间的函数，即：t=f(x,y,z,)等温面与等温线等温面与等温线某个瞬时时刻，温度场中相同温度各点连成的面称为等温面。对于维温度场某个瞬时时刻温度场中相同温度各点连对于二维温度场，某个瞬时时刻，温度场中相同温度各点连成的线称为等温线。例金属部件内的等温线例：金属部件内的等温线温度不同的等温面或等温线彼温度不同的等温面或等温线彼此不能相交；等温面上没有温差，不会有热传递传递；不同的等温面之间，有温差，有导热。温度梯度温度沿等温面（或等温线）法线方向的变化率与法向矢量乘积记为gradt或▽t温度梯度积，记为gradt,或▽t。注：温度变化率是标量；法向是矢量；温度梯度是矢量；由于矢量可以分解，温度梯度常用下式求解：温度梯度的另外几种定义度梯度朝着度增加最大的方向温度梯度朝着温度增加最大的方向；与等温面垂直，朝着温度增加的方向。热流量单位时间内，通过面积A的传递热量称为传热量，用表示，单位J/s或W。热流密度单位时间内，通过单位面积的热流量称为热流密度，用q表示，单位J/(m2s)或W/m2。密度，用q表示，单位J/(s)或/二、导热基本定律二、导热基本定律回忆热传导的定义；回忆热传导的定义；1822年，法国数学家傅里叶（Fourier）在实验研究基础上（而不1822年，法国数学家傅里叶（Fourier）在实验研究基础上（而不是理论推导），发现导热基本规律——傅里叶定律;大量实践经验表明，单位时间内通过单位横截面所传导的热量，正比于当地垂直于截面方向上的温度变化率，即，At比于当地垂直于截面方向上的温度变化率，即，Ax引入比例常数可得：二、导热基本定律二、导热基本定律ttt,,xyztttqqqxyx2-grad[Wm]qt或热导率（导热系数）W(m)K:注负号表热量传递的方向和度梯度的方向相反注：负号表示热量传递的方向和温度梯度的方向相反三热导率三、热导率物质的重要热物性参数q—物质的重要热物性参数gradt热导率的数值表征物质导热能力大小实验测定==xyz各向同性影响热率的因素物质的种类材料成分温度湿度热导率的数值表征物质导热能力大小。实验测定影响热率的因素：物质的种类、材料成分、温度、湿度、压力、密度等;金属非金属固相液相气相不同物质的导热系数概图不同物质热导率的差异：构造差别、导热机理不同不同物质热导率的差异：构造差别、导热机理不同1、气体的热导率0.006~0.6W(mK)气体0:0.0244W(m);CK空气20:0.026W(mK)C空气气体的导热：由于分子的热运动和相互碰撞时发生的能量传递2、液体的热导率007~07W(m)K0.07~0.7W(m)K液体20:0.6W(mK)C水液体的导热：主要依靠晶格的振动晶格：理想的晶体中分子在无限大空间里排列成周期性点晶格的晶体中分子在无限大间排列成周期性点阵，即所谓晶格大多数液体（分子量M不变）T大多数液体（分子量M不变）：水和甘油等强缔合液体分子量变化并随温度而变T水和甘油等强缔合液体，分子量变化，并随温度而变化。在不同温度下，热导率随温度的变化规律不一样液体的热导率随压力p的升高而增大pp3、固体的热导率(1)金属的热导率：12~418W(mK)金属纯金属的导热：依靠自由电子的迁移和晶格的振动主要依靠前者主要依靠前者金属导热与导电机理一致；良导电体为良导热体：银铜铝金T—晶格振动的加强干扰自由电子运动TCuCu10K:12000W(mK)15K:7000W(mK)(2)非金属的...