材料力学 第五章扭转应力(4,5)VIP免费

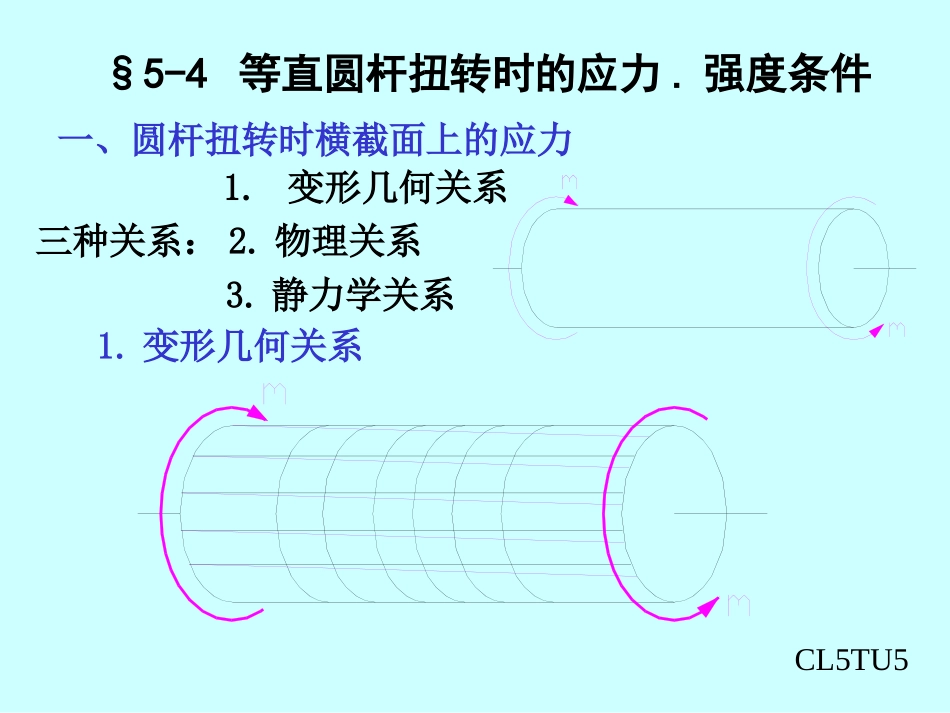
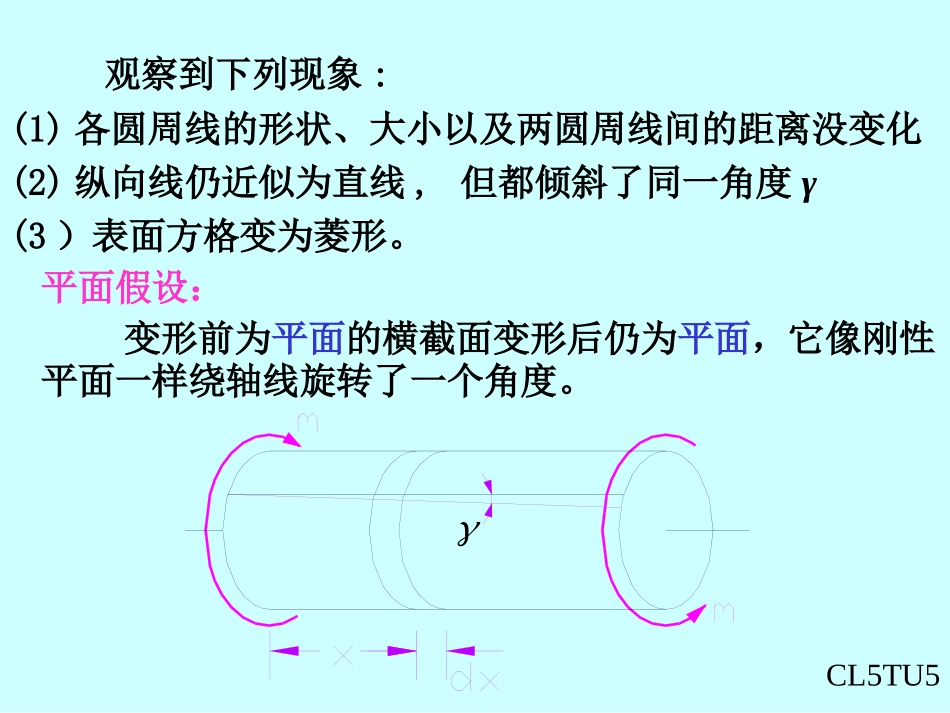
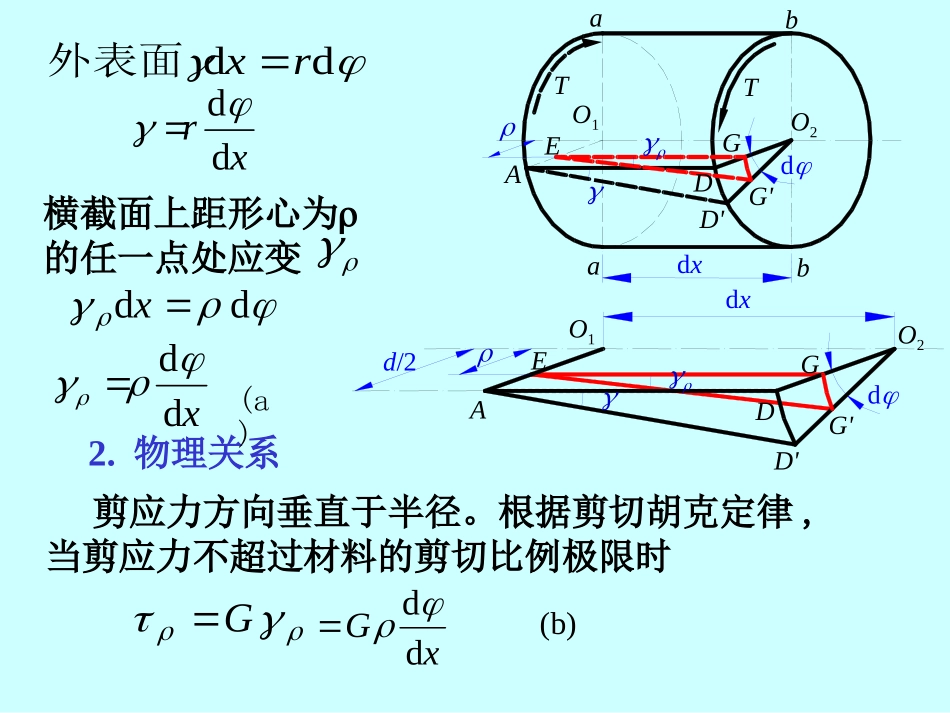
§5-4等直圆杆扭转时的应力.强度条件一、圆杆扭转时横截面上的应力1.变形几何关系三种关系：2.物理关系3.静力学关系CL5TU51.变形几何关系观察到下列现象:(1)各圆周线的形状、大小以及两圆周线间的距离没变化(2)纵向线仍近似为直线,但都倾斜了同一角度γ(3）表面方格变为菱形。平面假设：变形前为平面的横截面变形后仍为平面，它像刚性平面一样绕轴线旋转了一个角度。CL5TU5ddrx外表面ddxxddxrdd横截面上距形心为的任一点处应变剪应力方向垂直于半径。根据剪切胡克定律,当剪应力不超过材料的剪切比例极限时G2.物理关系Gxdd(a)(b)bbTTO1O2dGG'DD'aadxAEEAO1DdD'G'GO2d/2dx3.静力学关系TAAdTAxGAdddGxATAddd2pIGTxddIApA2d极惯性矩dAdAoTCL5TU9GxddmaxmaxTIppIGTGpITpWT)(maxpP抗扭截面模量IW由(b)式：opp.4WI和抗扭截面模量圆与圆环的极惯性矩324pdImaxpPIW2/pdId316D圆圆环4444p1323232DdDI43pmaxpP1162DDIIWdD[例5-2]内外径分别为20mm和40mm的空心圆截面轴，受扭矩T=1kN·m作用，计算横截面上A点的剪应力及横截面上的最大和最小剪应力。解：AApTI)5.01(3204.0015.0100044MPa66.63ApmaxWT)5.01(1604.0100043MPa88.84maxMPa44.422pminIdT[例5-5]一厚度为30mm、内直径为230mm的空心圆管，承受扭矩T=180kN·m。试求管中的最大剪应力，使用：(1)薄壁管的近似理论；(2)精确的扭转理论。解：(1)利用薄壁管的近似理论可求得trT2max216/)1(34maxDT(2)利用精确的扭转理论可求得16/29.0])290/230(1[1018034318010201300332..565.MPaMPa2.62max%9/)(maxmaxmax二.斜截面上的应力dxdyxn0F0cossinsincosdAdAdA2sin0F2cosmax45omin45o三.强度条件1.塑性与脆性材料的扭转破坏低碳钢平齐断口铸铁斜螺旋线断口2.强度条件][][pWT即(3)确定许可载荷:(1)校核杆的强度:已知T、Ip、，验算构件是否满足强度条件；][(2)设计截面:已知、,按强度条件，求A；max][CUIWAN.AVIRENWAN.AVI[例5-6]如图所示阶梯状圆轴，AB段直径d1=120mm，BC段直径d2=100mm。扭转力偶矩为MA=22kN.m，MB=36kN·m，Mc=14kN·m。已知材料的许用剪应力，试校核该轴的强度。MPa80][解：求得两段的扭矩，并绘出扭矩图。AB段之扭矩比BC段之扭矩大，但两段轴的直径不同，需要分别校核两段轴的强度。AB段][)(1084.6416/12.010226max33maxPaWTpⅠⅠⅠⅠBC段][)(103.7116/1.010146max33maxPaWTpⅡⅡⅡⅡ该轴满足强度条件的要求。§5-5圆轴的扭转变形与刚度条件一.扭转变形CL5TU5dddxTGIpddTGIxplpxGITdpIGlTT，则若constant公式适用条件：1）当p（剪切比例极限）公式才成立2）仅适用于圆杆（平面假设对圆杆才成立）3）扭矩、面积沿杆轴不变（T、Ip为常量）TGIxpld二.圆轴扭转时的刚度条件刚度条件：][ddpIGTx][180pGITradm//m。称为许可单位长度扭角][单位长度的扭角称为扭角率，用表示。对于精密机械)/(3.0~15.0][mo一般机械)/(2][mo图示钢制实心圆截面轴，已知：M1=1592N·m，M2=955N·m，M3=637N·m，lAB=300mm，lAC=500mm，d=70mm，钢的切变模量G=80GPa。试求横截面C相对于B的扭转角BC。(a)例题3-5ACB122(1)绘扭矩图kN.m212ABABTMMTkN.m41mTBCTX4-2(2)计算IP：[5-7]空心圆轴，外径Ｄ＝１００mm，内径ｄ＝８０mm，AB=l＝５００mm，M１＝4ｋＮ.m，M２＝6ｋＮ.m,Ｇ＝８０ＧＰａ，求C截面对A、B截面的相对扭转角。4644Pm108.532)1(DI解:(3)算相对扭角02693124.0)(10216.0108.5108010)42(5.0)(...