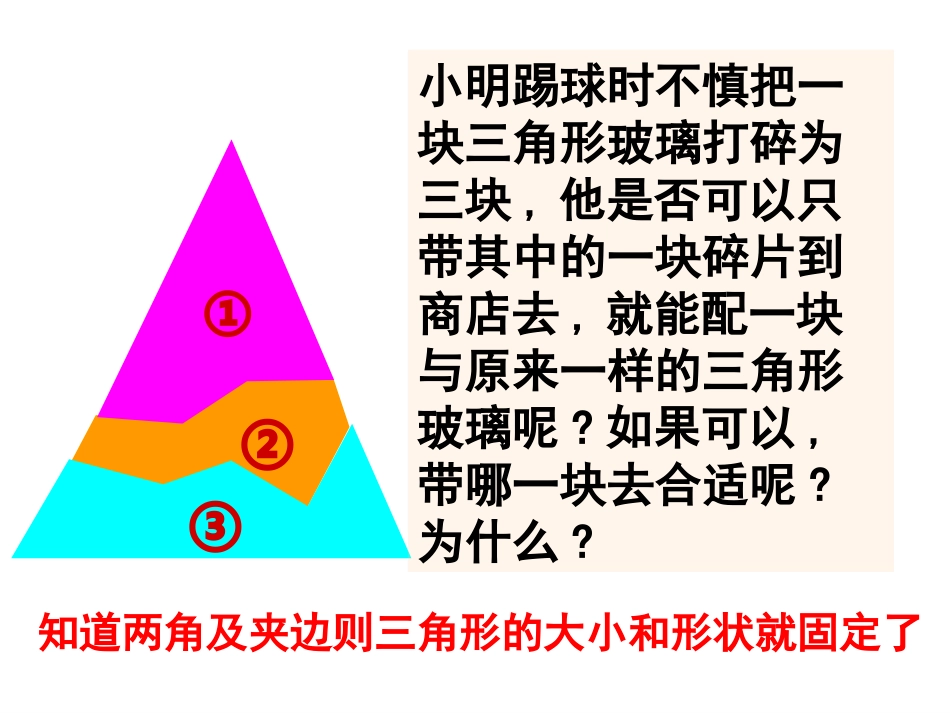
①②③小明踢球时不慎把一块三角形玻璃打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形玻璃呢?如果可以,带哪一块去合适呢?为什么?知道两角及夹边则三角形的大小和形状就固定了请大家用刻度尺,量角器(或圆规)画一个△ABC,使AB=4cm,∠A=30°,∠B=45°。用符号语言表达为:在△ABC与△DEF中∠A=D∠AB=DE∠B=E∠∴△ABCDEF≌△(ASA)ABCDEF两角和它们的夹边对应相等的两个三角形全等。简写成“角边角”或““ASA””例1:如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C。求证:BD=CE。ADECB证明:在△ACD和△ABE中∠A=A∠(公共角)AC=AB(已知)∠C=B∠(已知)∴△ACDABE≌△(ASA)∴AD=AE∴AB-AD=AC-AE即:BD=CE思考:如图,已知∠A=∠A’,B∠=∠B’,AC=A’C’,那么△ABC与△A’B’C’全等吗?你发现了什么?用符号语言表达为:在△ABC与△DEF中∠A=D∠∠B=E∠BC=EF∴△ABCDEF≌△(AAS)两角和其中一角的对边对应相等的两个三角形全等。简写成“角角边”或““AAS””ABCDEF(角边角ASA)(角角边AAS)三角形全等的判定3图19.2.91.已知:∠ABC=∠DCB,∠ACB=∠DBC,求证:△ABCDCB≌△.∠ABC=∠DCBBC=CB∠ACB=∠DBC证明:在△ABC和△DCB中,∴△ABCDCB≌△()ASA2.从C地看A、B两地的视角∠C是锐角,从C地到A、B两地的距离相等,A地到路段BC的距离AD与B地到路段AC的距离BE相等吗?为什么?到目前为止,我们一共探索出判定三角形全等的五种方法,它们分别是:2、边边边(SSS)4、角边角(ASA)5、角角边(AAS)3、边角边(SAS)1、定义2.如图∠1=∠2,∠B=∠D,求证△ABC≌△ADC.你也试一试:1.如图,要测量河两岸相对的两点A,B的距离,可以在AB的垂线BF上取两点C,D,使BC=CD,再定出BF的垂线DE,使A,C,E在一条直线上,这时测得DE的长就是AB的长。为什么?ABCDEF课本44页第5、6题作业作业作业作业•小组讨论:你能对三角形全等的判定方法做一个小结吗?•证明两个三角形全等的条件至少有一条边,三个角对应相等的两个三角形不一定全等,三边对应相等的两个三角形一定全等,两边和它们的夹角对应相等的两个三角形一定全等,两边和其中一边的对角对应相等的两个三角形不一定全等,两角和它们的夹边对应相等的两个三角形全等,两个角和其中一个角的对边对应相等的两个三角形全等。