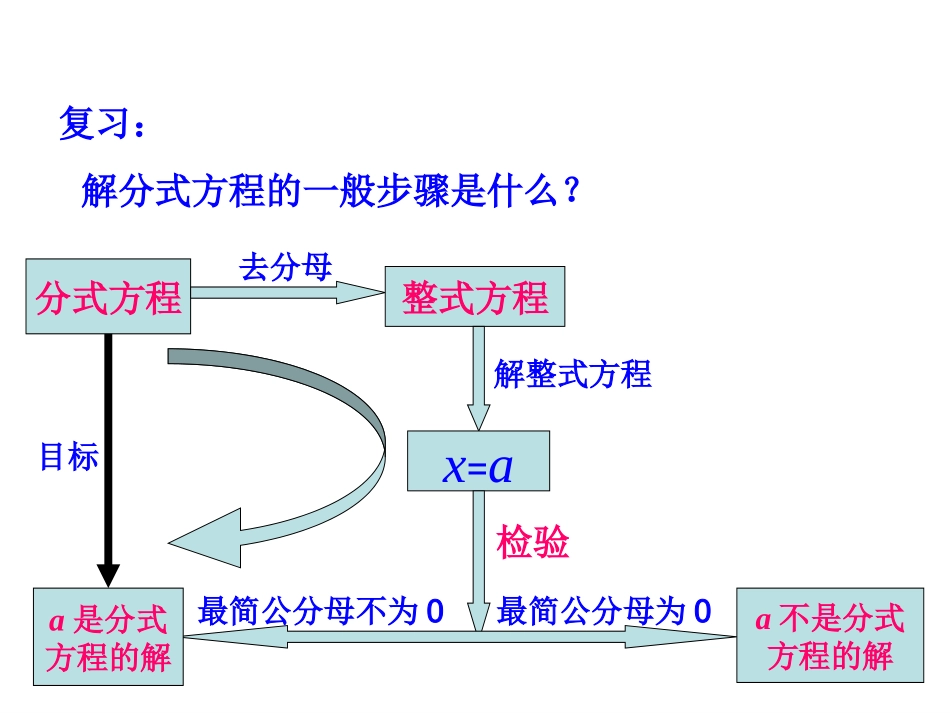
复习:解分式方程的一般步骤是什么?分式方程整式方程x=aa不是分式方程的解a是分式方程的解最简公分母不为0最简公分母为0检验解整式方程去分母目标1、工程问题基本量之间的关系:工作量=工作效率X工作时间常见等量关系:甲的工作量+乙的工作量=合作工作量注:工作问题常把总工程看作是单位1,水池注水问题也属于工程问题.`【【例例11】】两个工程队共同参与一项筑路工程,甲队单两个工程队共同参与一项筑路工程,甲队单独施工一个月完成总工程的三分之一,这时增加了乙独施工一个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成队,两队又共同工作了半个月,总工程全部完成..哪个队的施工速度快?哪个队的施工速度快?分式方程在实际在应用分式方程在实际在应用解:解:设乙队如果单独施工一个月能完成总工程的设乙队如果单独施工一个月能完成总工程的..x1记总工程量为记总工程量为11,根据题意,得,根据题意,得3161x21=1解得解得1x检验:当检验:当xx=1=1时,时,6X6X≠0。所以,原分式方程的解为所以,原分式方程的解为X=1X=1由上可知,若乙队单独工作一个月可以完成全部任务,由上可知,若乙队单独工作一个月可以完成全部任务,所以乙队施工速度快所以乙队施工速度快..1、一项工程,若甲单独做,刚好在规定日期内完成,苦乙单做,则要超过规定时间6天完成;现甲乙两人合作4天后,剩下工程由乙单独做,刚好在规定日期内完成。问规定日期是几天?2、甲、乙两人每时共能做35个零件,当甲做了90个零件时,乙做了120个。问甲、乙每时各做多少个机器零件?解:设甲每小时做X个,乙每小时做(35-x)个,则xx35120902、甲加工180个零件所用的时间,乙可以加工240个零件,已知甲每小时比乙少加工5个零件,求两人每小时各加工的零件个数.解:设乙每小时加工x个,甲每小时加工(x-5)个,则xx2405180解得x=20检验:x=20时x(x-5)≠0,x=20是原分式方程的解。答:乙每小时加工20个,甲每小时加工15个。x-5=153、一个水池有甲、乙两个水管,甲管注满水池的时间是乙管的2倍。如果单独开放甲管5小时,再单独开放乙管6小时,就可以注满水池的一半,求单独开放一个水管,注满水池各需多少时间?3、某工人师傅先后两次加工零件各1500个,当第二次加工时,他革新了工具,改进了操作方法,结果比第一次少用了18个小时.已知他第二次加工效率是第一次的2.5倍,求他第二次加工时每小时加工多少零件?解:设他第一次每小时加工x个,第二次每小时加工2.5x个,则185.215001500xx常见题型及相等关系2、行程问题:基本量之间的关系:路程=速度X速度,即s=vt常见的相等关系:(1)、相遇问题:甲行程+乙行程=全路程(2)、追及问题:(设甲的速度快)1)、同时不同地:甲用的时间=乙用的时间甲的行程-乙的行程=甲乙原来相距的路程2)、同地不同时:甲用的时间=乙用的时间-时间差甲走的路程=乙走的路程3)、水(空)航行问题:顺流速度=静水中航速+水速逆流航速=静水中速度–水速【【例例22】】从从20042004年年55月起某列车平均提速月起某列车平均提速vv千千米米//小时,用相同的时间,列车提速前行驶小时,用相同的时间,列车提速前行驶ss千千米,提速后比提速前多行驶米,提速后比提速前多行驶5050千米,提速前列千米,提速前列车的平均速度为多少?车的平均速度为多少?解:设提速前的速度为x,提速后为x+v,则vxsxs50解得50svx50svx50svx检验:时,x(x+v)≠0,是方程的解。50sv答:提速前列车的平均速度为千米/小时。1、一队学生去校外参观,他们出发30分钟时,学校要把一个紧急通知传给带队老师,派一名学生骑车从学校出发,按原路追赶队伍.若骑车的速度是队伍行进速度的2倍,这名学生追上队伍时离学校的距离是15千米,问这名学生从学校出发到追上队伍用了多少时间?解:设队伍的速度为x,骑车的速度为2x,则603021515xx解得x=15经检验x=15是原方程的解。5.0215x答:这名学生追上队伍用了0.5小时。2、某人骑自行车比步行每小时多走8千米,如果他步行12千米所用时间与骑车行36千米所用的时间相等,求他步行40千米用多少小时?解:设步行每小时行x千米...