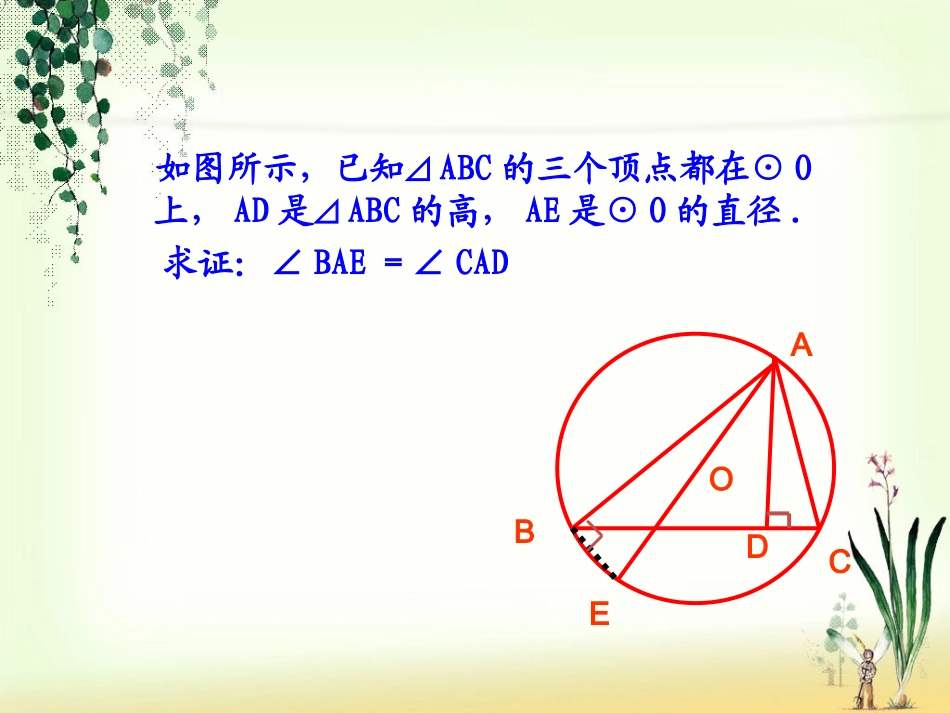
24.1.4圆周角第2课时第二课时应用•回顾:圆周角定理及推论?•思考:判断正误:1.同弧或等弧所对的圆周角相等()2.相等的圆周角所对的弧相等()3.90°角所对的弦是直径()4.直径所对的角等于90°()5.长等于半径的弦所对的圆周角等于30°()ABECOD如图所示,已知⊿ABC的三个顶点都在⊙O上,AD是⊿ABC的高,AE是⊙O的直径.求证:∠BAE=∠CAD例如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.86102222ACABBC又在Rt△ABD中,AD2+BD2=AB2,221052(cm)22ADBDAB解:∵AB是直径,∴∠ACB=∠ADB=90°.在Rt△ABC中,∵CD平分∠ACB,∴AD=BD..ACDBCD例题OABCD3.求证:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.(提示:作出以这条边为直径的圆.)·ABCO求证:△ABC为直角三角形.证明:CO=AB,12以AB为直径作⊙O,∵AO=BO,∴AO=BO=CO.∴点C在⊙O上.又∵AB为直径,∴∠ACB=×180°=90°.12已知:△ABC中,CO为AB边上的中线,12且CO=AB∴△ABC为直角三角形.课本练习课堂练习•1.如图,OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC,∠ACB与∠BAC的大小有什么关系?为什么?OABC•2.如图,A、B、C、D是⊙O上的四个点,且∠BCD=100°,求∠BOD(所对的圆心角)和∠BAD的大小。OBDCA探究3、如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC交⊙O于点F,点F不与点A重合。(1)AB与AC的大小有什么关系?为什么?(2)按角的大小分类,请你判断△ABC属于哪一类三角形,并说明理由。ACBDF·O∴△ABC是锐角三角形解:(1)AB=AC。证明:连接AD又∵DC=BD,∴AB=AC。(2)△ABC是锐角三角形。由(1)知,∠B=C∠<90°连接BF,则∠AFB=90°,∴∠A<90°∵AB是直径,∴∠ADB=90°,1.AB、AC为⊙O的两条弦,延长CA到D,使AD=AB,如果∠ADB=35°,求∠BOC的度数。⌒⌒2、如图,在⊙O中,BC=2DE,∠BOC=84°,求∠A的度数。∠BOC=140°∠A=21°4、在⊙O中,一条弧所对的圆心角和圆周角分别为(2x+100)°和(5x-30)°,则x=__;3.如图,在直径为AB的半圆中,O为圆心,C、D为半圆上的两点,∠COD=50°,则∠CAD=______;20°50°拓展练习如图,点P是⊙O外一点,点A、B、Q是⊙O上的点。(1)求证∠P<∠AQB(2)如果点P在⊙O内,∠P与∠AQB有怎样的关系?为什么?OBpQA