理论力学动静法VIP免费

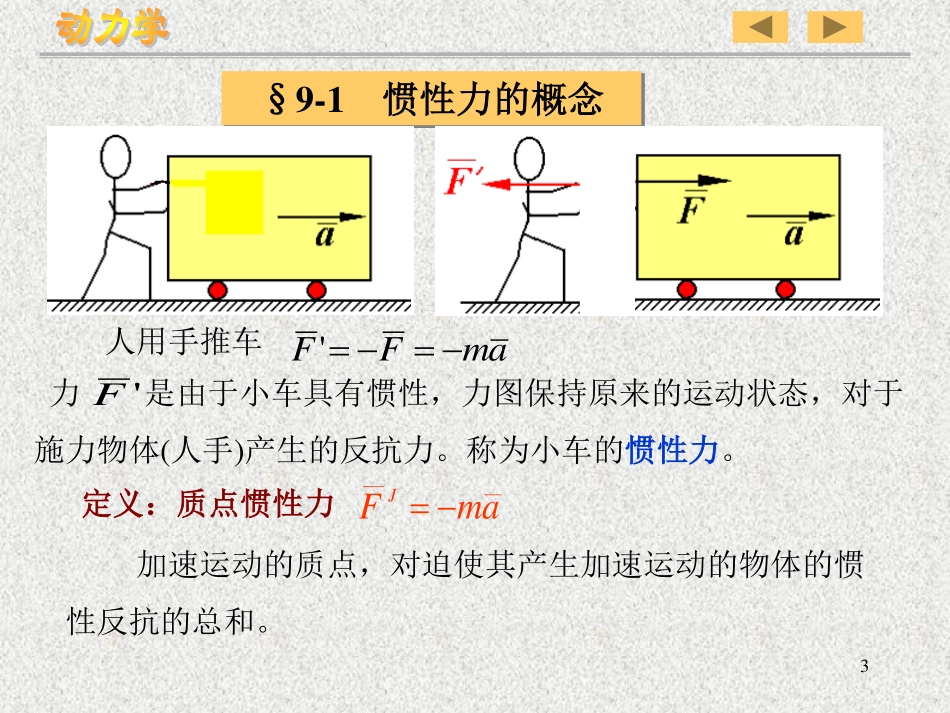
2动力学普遍定理，是解决动力学问题的普遍方法，在一定条件下也是简捷而有效的方法。本章介绍解答动力学问题的另一种方法——达兰贝尔原理或译为达朗伯原理。应用这一原理，就将动力学问题从形式上转化为静力学问题，从而根据关于平衡的理论来求解。这种解答动力学问题的方法，因而也称动静法。3§9-1惯性力的概念人用手推车amFF'力是由于小车具有惯性，力图保持原来的运动状态，对于施力物体(人手)产生的反抗力。称为小车的惯性力。'F定义：质点惯性力加速运动的质点，对迫使其产生加速运动的物体的惯性反抗的总和。amFJ4zJzyJyxJxamFamFamF③惯性力作用在使质点产生加速度的其他施力物体上。①大小：FJ=maJF②方向：与相反aJF按不同坐标系，惯性力可分解为：0bJbnJnJamFamFamF——切向惯性力——法...............5NFR0JFNF这就是质点的达兰贝尔原理。§9-2达兰贝尔原理非自由质点M，质量m，受主动力，约束反力作用，、的合力为FNFN由牛顿第二定律：amR假象地将作用在M上，则JF0amamFRJJF即：一、质点的达兰贝尔原理6该方程对动力学问题来说只是形式上的平衡，并没有改变动力学问题的实质。采用动静法解决动力学问题的最大优点，就是可以利用静力学提供的解题方法，给动力学问题一种统一的解题格式。也就是：对于动力学问题，假想地加上惯性力，就可以用平衡方程求解。7[例1]列车在水平直线轨道上行驶，车厢内悬挂一单摆，当车厢向右作匀加速运动时，单摆左偏角度，相对于车厢静止。求车厢的加速度。a8研究对象：单摆的摆锤虚加惯性力maFJ0cossin,0JFmgXtgga角随着加速度的变化而变化，当不变时，角也不变。只要测出角，就能知道列车的加速度。摆式加速计的原理。aaa解：得方向与相反a0cossinmamg即：9对整个质点系，如果在每一个质点上都假象地加上惯性力，则主动力系、约束反力系、惯性力系在形式上构成平衡力系。这就是质点系的达兰贝尔原理。可用方程表示为：0)()()(0JiOiOiOJiiiFmNmFmFNF设有一质点系由n个质点组成，对任一质点，虚加惯性力，则有),1,2,......(0niFNFJiii二、质点系的达兰贝尔原理对于每一个研究对象，平面问题有三个平衡方程，空间问题有六个平衡方程。10§9-3刚体惯性力系的简化一般质点系，在应用动静法是，可在每一质点上虚加相应的惯性力，但对于刚体这样由无穷多质点组成的质点系，则不可能逐个质点虚加惯性力。怎么办？可以采用静力学中的力系简化的理论，求出各质点惯性力所组成的惯性力系的主矢和主矩，来代替惯性力系。这样，在刚体上虚加了惯性力系的主矢和主矩，就相当于在刚体上的各个质点上虚加了惯性力。11一、刚体作平动惯性力系向质心C简化：CCiiiJiJaMamamFF)(0)(CCCiiCiiJiiJCarMarmamrFrM0,JCcJMaMF故刚体平动时惯性力系合成为一过质心的合惯性力。质心相对于质心的矢径相对于质心的矢径0,CiirMr12空间惯性力系—>平面惯性力系（质量对称面）O为转轴z与质量对称平面的交点，向O点简化：iiJiamF主矢：主矩：CiiJiJaMamFF)(二、定轴转动刚体设刚体具有垂直于转轴的质量对称平面。O直线i：平动，过Mi点，JiFJinF)(0)()(2反向负号表示与OiiiiiJinOJiOJOJrmrmrFmFmM13即：向O点简化：CJaMFOJOJM作用在O点作用在C点CJaMFCJCJM若向质心C简化，同理可得实际应用时可将惯性主矢分解：JnJcnccncCJFFaMaMaaMaMF)(14讨论：①若ε=0，转轴不通过质点C，向转轴简化，则0,JOCnCJMaMaMF②若转轴过质点C，且0，则OJOJJMF,0③若ε=0且转轴过质心C，则0,0JOJMF15假设刚体具有质量对称平面，并且平行于该平面作平面运动。此时，刚体的惯性力系可先简化为对称平面内的平面力系。刚体平面运动可分解为随基点（质点C）的平动：绕通过质心轴的转动：CJaMFCJCJM三、刚体作平面运动CJaMFCJCJM...