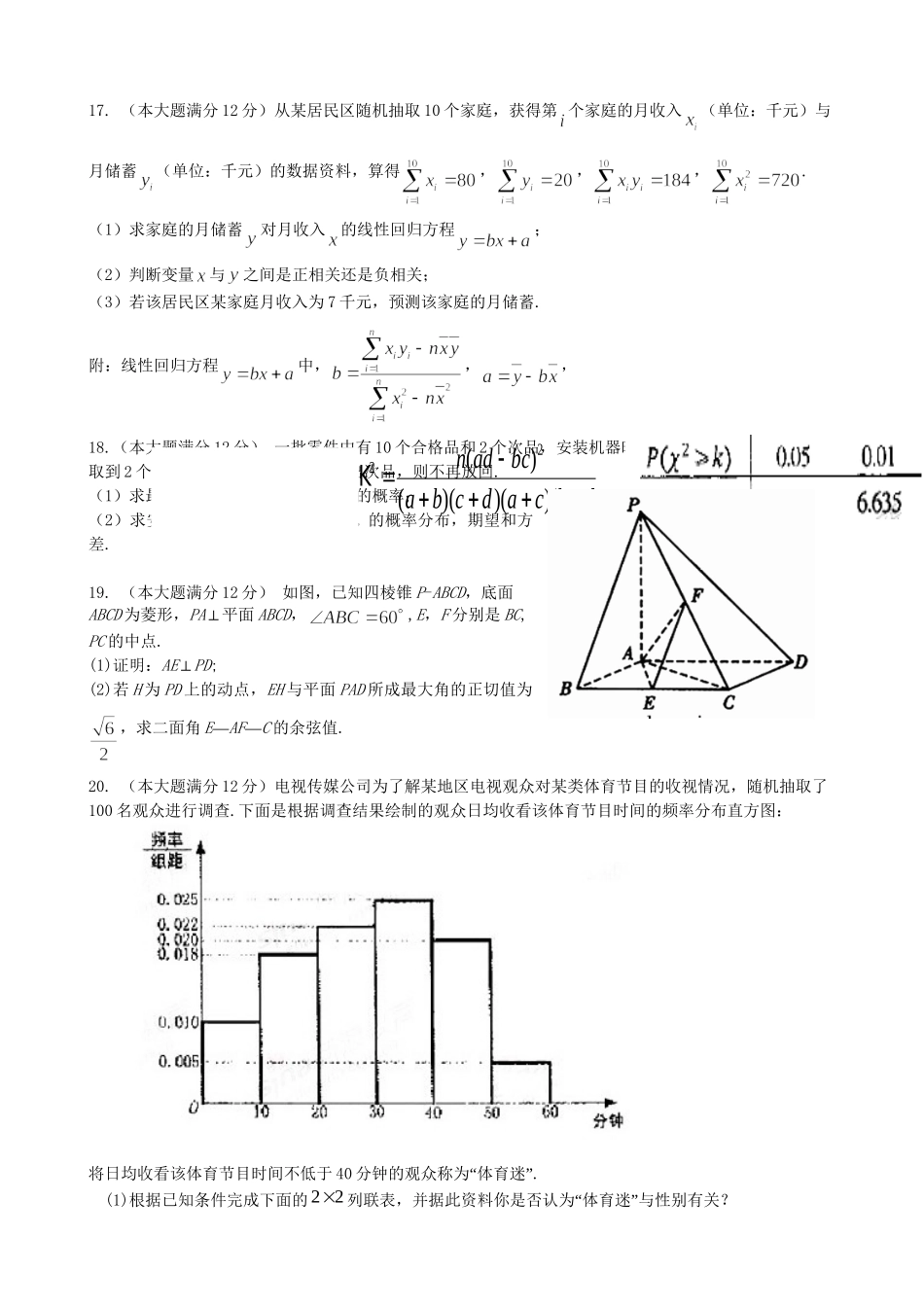
-学年第二学期期末联考试卷高二理科数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两卷,满分150分,考试时间120分钟。第Ⅰ卷一、选择题(本大题共12个小题,每小题5分,共60分)1.如果的方差为3,那么2.2.2.2.2.2的方差是A.0B.3C.6D.122.某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:第一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒;……第六组,成绩大于等于18秒且小于19秒。右图是按上述分组方法得到的频率分布直方图。设成绩小于17秒的学生人数占全班总人数的百分比为,成绩大于等于15秒且小于17秒的学生人数为,则从频率分布直方图中可分析出和分别为A.B.C.D.3.在(x-)10的展开式中,x4的系数为A.-120B.120C.-15D.154.有两排座位,前排11个座位,后排12个座位,现安排2人就座,规定前排中间的3个座位不能坐,并且这2人不左右相邻,那么不同排法的种数是A.234B.346C.350D.3635.如图,在圆心角为直角的扇形OAB中,分别以OA,OB为直径作两个半圆。在扇形OAB内随机取一点,则此点取自阴影部分的概率是A.B.C.D.6.已知随机变量服从正态分布,,则A.B.C.D,7.设集合I={1,2,3,4,5},选择I的两个非空子集A和B,要使B中的最小的数大于A中最大的数,则不同的选择方法共有A.50种B.49种C.48种D.47种8.A.-1B.-2C.-512D.5109.设a>b>1,0c,给出下列三个结论:①ca>cb;②ca<cb;③log()log()baacbc.其中所有的正确结论的序号是.A.①B.①②C.②③D.①②③10.则至少有一次五人全部击中目标的概率是11.如图,网格纸上小正方形的边长为,粗线画出的是某几何体的三视图,则此几何体的体积为A.B.C.D.12.一平面截一球得到直径是6cm的圆面,球心到这个平面的距离是4cm,则该球的体积是A.B.C.D.第Ⅱ卷二、填空题(本大题共4小题,每小题5分,共20分)13.甲、乙两人在10天中每天加工零件的个数用茎叶图表示如下图,中间一列的数字表示零件个数的十位数,两边的数字表示零件个数的个位数,则这10天甲、乙两人日加工零件的平均数分别为和.14.已知x、y的取值如下表所示x0134y2.24.34.86.7从散点图分析,y与x线性相关,且,则__________15.任取实数a,b1,1,则a,b满足22ab的概率为__________.16.甲罐中有5个红球,2个白球和3个黑球,乙罐中有4个红球,3个白球和3个黑球.先从甲罐中随机取出一球放入乙罐,分别以12,AA和3A表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以B表示由乙罐取出的球是红球的事件,则下列结论中正确的是________(写出所有正确结论的编号).①25PB;②15|11PBA;③事件B与事件1A相互独立;④123,,AAA是两两互斥的事件;⑤PB的值不能确定,因为它与123,,AAA中哪一个发生有关.三、解答题:本大题共6个小题,共70分,解答应写出文字说明、证明过程或演算步骤。17.(本大题满分12分)从某居民区随机抽取10个家庭,获得第个家庭的月收入(单位:千元)与月储蓄(单位:千元)的数据资料,算得,,,.(1)求家庭的月储蓄对月收入的线性回归方程;(2)判断变量与之间是正相关还是负相关;(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.附:线性回归方程中,,,18.(本大题满分12分)一批零件中有10个合格品和2个次品,安装机器时从这批零件中逐个任选,取取到2个合格品才能安装成功,若取出次品,则不再放回.(1)求最多取3次零件就能安装成功的概率;(2)求安装成功前已取出的次品数ξ的概率分布,期望和方差.19.(本大题满分12分)如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,,E,F分别是BC,PC的中点.(1)证明:AE⊥PD;(2)若H为PD上的动点,EH与平面PAD所成最大角的正切值为,求二面角E—AF—C的余弦值.20.(本大题满分12分)电视传媒公司为了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:将日均收看该体育节目时间不低于40“”分钟的观众称为体育迷.(1)根据已知条件完成下面的22“”列联表,并据此资...