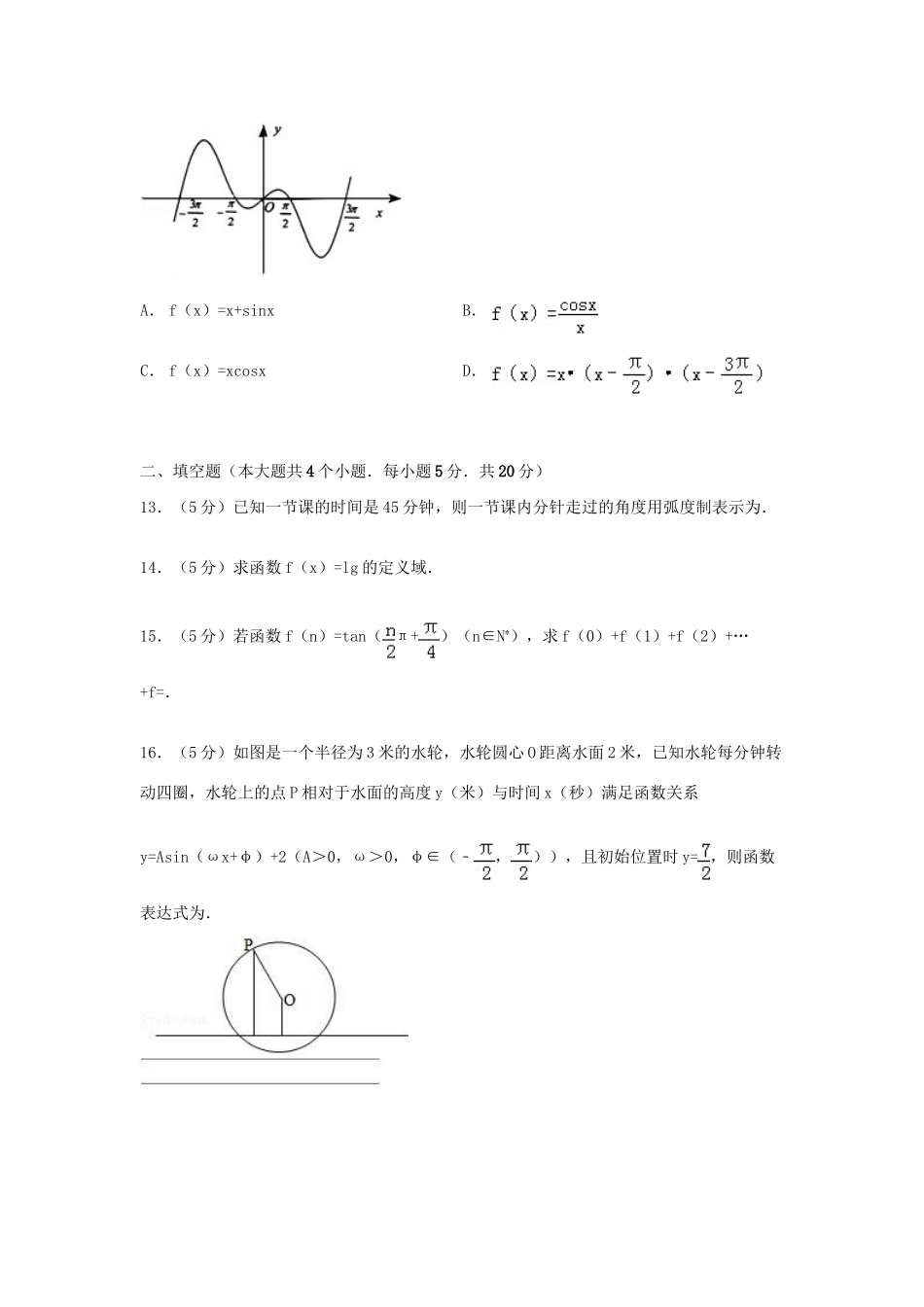
江西省南昌市八一中学、洪都中学、麻丘中学-学年高一上学期1月联考数学试卷一、选择题:(大题共12题,每小题5分,共60分四个选项中只有一个正确答案)1.(5分)已知A={第一象限角},B={锐角},C={小于90°的角},那么A、B、C关系是()A.B∪C=CB.B=A∩CC.A⊊CD.A=B=C2.(5分)若点P在的终边上,且|OP|=2,则点P的坐标()A.(1,﹣)B.(,﹣1)C.(﹣1,﹣)D.(﹣1,)3.(5分)若α是第四象限的角,则π﹣α是()A.第一象限的角B.第二象限的角C.第三象限的角D.第四象限的角4.(5分)sin2cos3tan4的值()A.小于0B.大于0C.等于0D.不存在5.(5分)为了得到函数的图象,只需把函数的图象()A.向左平移个单位长度B.向左平移个单位长度C.向右平移个单位长度D.向右平移个单位长度6.(5分)已知弧度数为2的圆心角所对的弦长也是2,则这个圆心角所对的弧长是()A.2B.C.2sin1D.sin27.(5分)设、、,则它们的大小关系为()A.a<c<bB.b<c<aC.a<b<cD.b<a<c8.(5分)给出如下四个函数①f(x)=5sin(x﹣)②f(x)=cos(sinx)③f(x)=xsin2x④f(x)=其中奇函数的个数是()A.1个B.2个C.3个D.4个9.(5分)函数f(x)=给出下列四个命题,其中正确的是()A.f(x)的值域为B.f(x)是以π为周期的周期函数C.当且仅当x=2kx+(k∈Z)时,f(x)取得最大值D.当且仅当2kx+π<x<2kx+((k∈Z))时,f(x)<010.(5分)若实数x满足㏒2x=1+sinθ,则|x﹣4|+|x+1|=()A.2x﹣3B.3﹣2xC.﹣3D.511.(5“”分)用五点法画函数f(x)=Asin(ωx+φ)的简图时,若所得五个点的横坐标从小到大依次为等于()A.B.πC.D.2π12.(5分)函数f(x)的部分图象如图所示,则f(x)的解析式可以是()A.f(x)=x+sinxB.C.f(x)=xcosxD.二、填空题(本大题共4个小题.每小题5分.共20分)13.(5分)已知一节课的时间是45分钟,则一节课内分针走过的角度用弧度制表示为.14.(5分)求函数f(x)=lg的定义域.15.(5分)若函数f(n)=tan(π+)(n∈N*),求f(0)+f(1)+f(2)+…+f=.16.(5分)如图是一个半径为3米的水轮,水轮圆心O距离水面2米,已知水轮每分钟转动四圈,水轮上的点P相对于水面的高度y(米)与时间x(秒)满足函数关系y=Asin(ωx+φ)+2(A>0,ω>0,φ∈(﹣,)),且初始位置时y=,则函数表达式为.三、解答题(本大题共6小题,17题10分,其它每题12分,共70分,解答题应根据要求写出必要的文字说明.证明过程或演算步骤)17.(10分)计算:﹣(1﹣cos2585°•)tan(﹣π).18.(12分)角α的终边上的点P到x轴的距离与到y轴的距离之比是,求3sinα﹣cosα的值.19.(12分)已知cosα是方程6x2﹣7x﹣3=0的根,求的值.20.(12分)设函数f(x)=sin(2x+φ)(﹣π<φ<0),y=f(x)图象的一条对称轴是直线.(Ⅰ)求φ;(Ⅱ)求函数y=f(x)的单调增区间;(Ⅲ)画出函数y=f(x)在区间上的图象.21.(12分)设函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,﹣π<φ<π)的一个最高点坐标为(,3),其图象与x轴的相邻两个交点的距离为.(1)求f(x)的最小正周期及解析式;(2)若x∈从而弧长为α•r=,故选B.点评:本题考查弧长公式的应用,解直角三角形求出扇形的半径AO的值,是解决问题的关键.7.(5分)设、、,则它们的大小关系为()A.a<c<bB.b<c<aC.a<b<cD.b<a<c考点:对数值大小的比较.专题:计算题;综合题.分析:确定tan70°、sin25°、cos25°的范围,根据对数函数的性质,指数函数的性质,确定a、b、c的大小.解答:解:因为tan70°>1,所以<0sin25°<,所以>1因为<cos25°<1,所以0<<1所以a<c<b故选A.点评:本题考查对数值大小的比较,是基础题.8.(5分)给出如下四个函数①f(x)=5sin(x﹣)②f(x)=cos(sinx)③f(x)=xsin2x④f(x)=其中奇函数的个数是()A.1个B.2个C.3个D.4个考点:函数奇偶性的判断.专题:函数的性质及应用.分析:利用函数的奇偶性定义分别对四个函数分析解答.解答:解:对于①是非奇非偶的函数;对于②f(...