新课标人教A版必修4厦门市—学高中数学练习（二）B(1.4、1.5、1.6)VIP免费

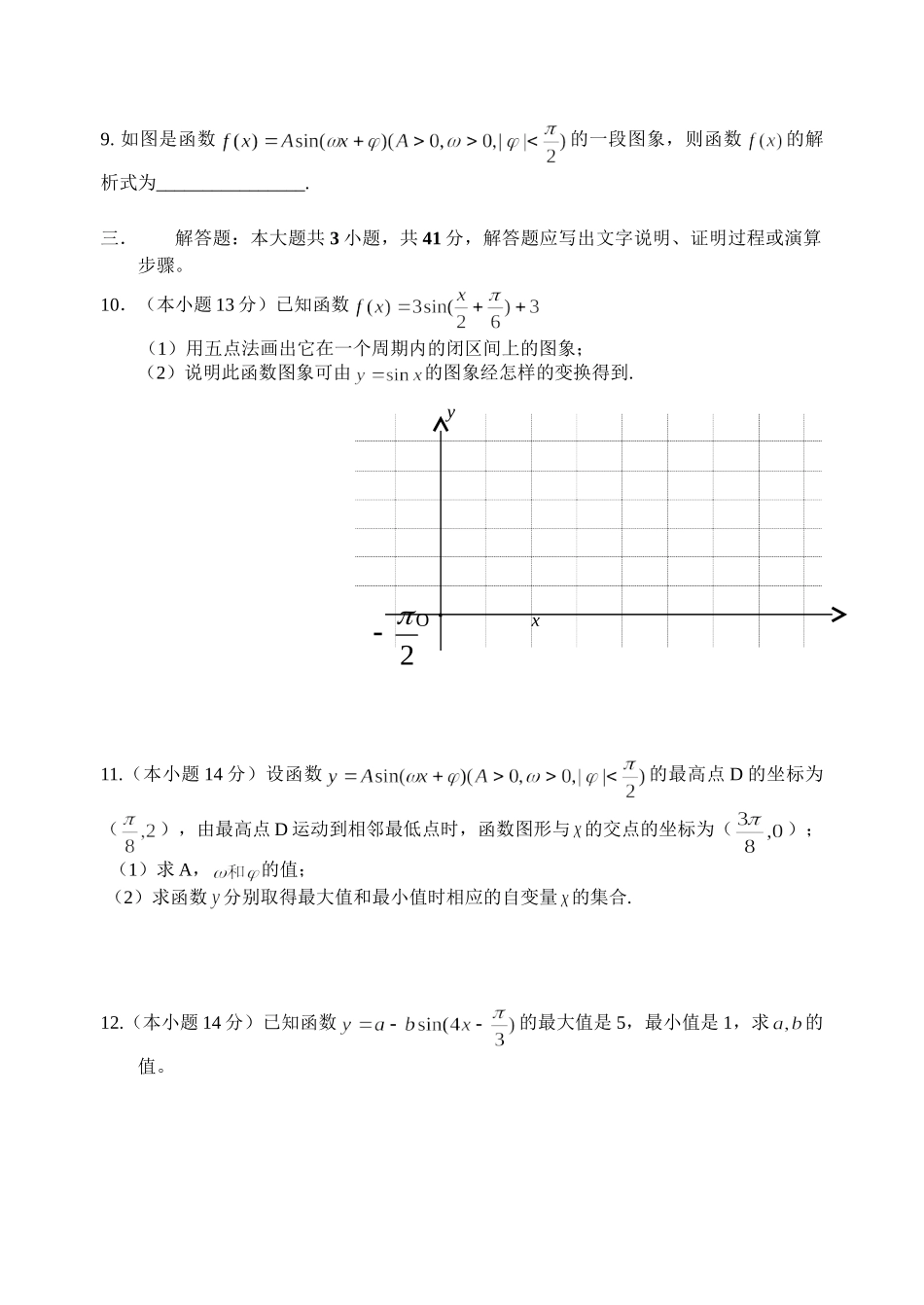
厦门市—学年数学必修4练习（二）B适用范围1.4三角函数图象与性质，1.5函数的图象，1.6三角函数模型的简单应用A组题（共100分）一．选择题：本大题共5小题，每小题7分，共35分。在每小题给出的四个选项中，只有一项是符合题目要求的。1.函数的周期为（）A.B.C.D.2.函数的图象大致为（）ABCD3.设集合，，则（）A.B.C.D.4.函数是（）A.偶函数B.奇函数C.非奇非偶的函数D.既是奇函数又是偶函数5.将函数的图象的各点向左平移、向上平移1个长度单位后，的到的图象对应的函数解析式是（）A.B.C.D.二．填空题：本大题共4小题，每小题6分，共24分。6．比较的大小，则_________________；7.函数的定义域为___________________;8.函数的图象的对称轴方程是_____________;|||||Ox||y|||||Ox||y|||||Ox||y|||||Ox||yOxy2-29.如图是函数的一段图象，则函数的解析式为________________.三．解答题：本大题共3小题，共41分，解答题应写出文字说明、证明过程或演算步骤。10．（本小题13分）已知函数（1）用五点法画出它在一个周期内的闭区间上的图象；（2）说明此函数图象可由的图象经怎样的变换得到.11.（本小题14分）设函数的最高点D的坐标为（），由最高点D运动到相邻最低点时，函数图形与的交点的坐标为（）；（1）求A，的值；（2）求函数分别取得最大值和最小值时相应的自变量的集合.12.（本小题14分）已知函数的最大值是5，最小值是1，求的值。Oxy2B组题（共100分）四．选择题：本大题共5小题，每小题7分，共35分。在每小题给出的四个选项中，只有一项是符合题目要求的。13．在中，已知,那么下列结论一定成立的是（）A.B.C.D.14.函数的图象在y周右侧与x的第一个交点的横坐标为（）A.B.C.D.15..函数的最小正周期是（）A.B.C.D.16.函数的单调增区间为（）A.B.C.D.17．函数的图象的一个对称中心是（）A.（）B.C.D.五．填空题：本大题共4小题，每小题6分，共24分。18．若函数的图象与直线围成一个封闭的平面图形，则这个封闭图形的面积为______________________；19.当时，函数的最小值为________________；20.直线与正切曲线相交的两个相邻的交点的距离为______.21.设函数是以2为最小正周期的函数，且是，，则＝____________；六．解答题：本大题共3小题，共41分，解答题应写出文字说明、证明过程或演算步骤。22．（本小题13分）若时，的值总大于零，求实数的取值范围.xy1-O23．（本小题14分））已知函数一段的图象过点（0，1），如图所示。（1）求函数的解析式；（2）将函数的图象向右平移个单位，得到的图象，求的单调减区间.24.（本小题14分）已知函数。（1）在直角坐标系中作出函数的大约图象；（2）讨论其值域、奇偶性和单调性，并加以证明.C组题（共50分）七．选择或填空题：本大题共2题。25．定义在上函数既是偶函数又是周期函数，若的最小正周期是，且当时，，则的值为（）A.B.C.D.26对于,有一个对称中心是（）的函数可能是（）A.B.C.D.八．解答题：本大题共2小题，解答题应写出文字说明、证明过程或演算步骤。27．设函数.（1）写出的最大值M，最小值m，最小正周期T；（2）试求最小正整数k，使得当自变量x在任意两个整数间（包括整数本身）变化时，函数至少有一个值是M和一个值是m.28．下表是某地一年中10天测量得白昼时间统计表（时间近似0.1小时，一年按365天计）日期1月1日2月28日3月21日4月27日5月6日6月21日8月13日9月20日10月25日12月21日日期位置序号x15980117126172225263298355白昼时间y(小时)5.610.212.416.417.319.416.412.48.55.4（1）以日期在365天中得位置序号x为横坐标，白昼时间y为纵坐标，在给定得坐标系中，试选用一个形如的函数来近似描述一年中，白昼时间y与日期位置序号x之间得函数关系；（2）用（1）中得函数模型估计该地一年中大约有多少天白昼时间大于15.9小时。厦门市—学年数学必修4练习（二）参考答案A组题（共100分）一.选择题：ADABD二.填空题：6.7.8.9..三.解答题：10．解：（1）列表x62x0y36303Oxy2（2）①由的图象上各点向左平移个长度单位，得的图象；②由的图象上各点的横坐标伸长为原来的2倍（纵坐标不变），得的图象；③由的图象上各点...