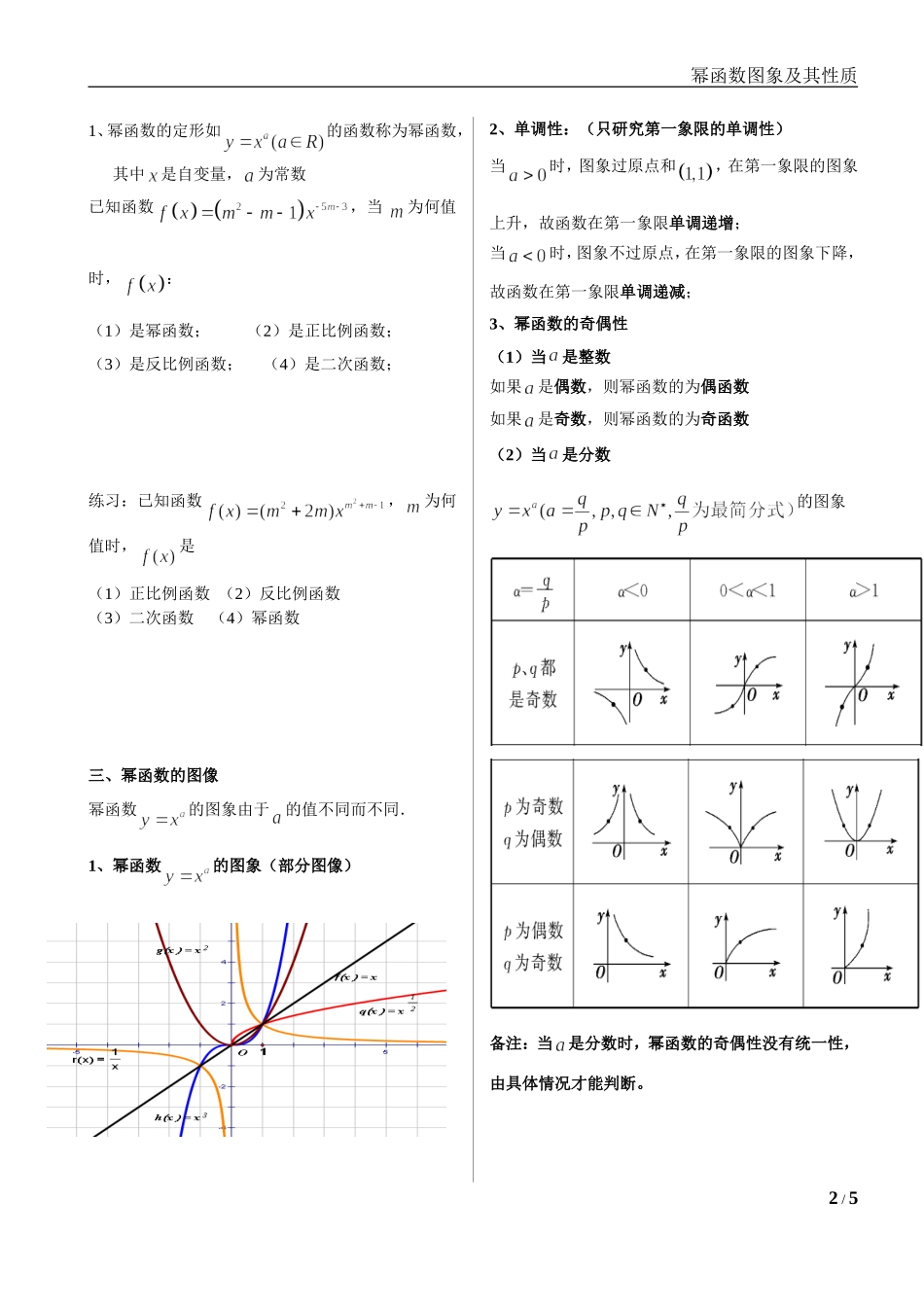
幂函数图象及其性质幂函数的图像与性质一、根式与有理数指数幂1、根式(1)根式的概念根式的概念符号表示备注如果,那么叫做的次方根当为奇数时,正数的次方根是一个正数,负数的次方根是一个负数零的次方根是零当为偶数时,正数的次方根有两个,它们互为相反数负数没有偶次方根(2)两个重要公式①;②(注意必须使有意义)。2、有理数指数幂(1)幂的有关概念①正数的正分数指数幂:②正数的负分数指数幂:③0的正分数指数幂为0,0的负分数指数幂无意义.注:分数指数幂与根式可以互化,通常利用分数指数幂进行根式的运算。(2)有理数指数幂的性质①;②;③;例2(1)计算:;(2)化简:二、幂函数1/5n为奇数n为偶数幂函数图象及其性质1、幂函数的定形如的函数称为幂函数,其中是自变量,为常数已知函数,当为何值时,:(1)是幂函数;(2)是正比例函数;(3)是反比例函数;(4)是二次函数;练习:已知函数,为何值时,是(1)正比例函数(2)反比例函数(3)二次函数(4)幂函数三、幂函数的图像幂函数的图象由于的值不同而不同.1、幂函数的图象(部分图像)2、单调性:(只研究第一象限的单调性)当时,图象过原点和,在第一象限的图象上升,故函数在第一象限单调递增;当时,图象不过原点,在第一象限的图象下降,故函数在第一象限单调递减;3、幂函数的奇偶性(1)当是整数如果是偶数,则幂函数的为偶函数如果是奇数,则幂函数的为奇函数(2)当是分数的图象备注:当是分数时,幂函数的奇偶性没有统一性,由具体情况才能判断。2/5幂函数图象及其性质4、幂的大小与函数图像的关系总结:在直线右侧,图像越靠近轴,幂越小;练习、右图为幂函数在第一象限的图像,则的大小关系是()题型分析:一、求定义域1、函数的定义域为.2、函数y=(x2-2x)的定义域3、求函数25yx的定义域练习:1、若a<a,则a的取值范围是()A.a≥1B.a>0C.1>a>0D.1≥a≥02、若<,求则a的取值范围二、单调性1、函数y=的单调递减区间为()A.(-∞,1)B.(-∞,0)C.[0,+∞]D.(-∞,+∞)下列函数在上为减函数的是()A.B.C.D.三、判断下列函数的奇偶性1、已知幂函数,那么函数为A.奇函数B.偶函数C.非奇非偶函数D.减函数2、已知幂函数25yx,那么函数为A.奇函数B.偶函数C.非奇非偶函数D.减函数3、已知幂函数f(x)=x(m∈Z)为偶函数,且在区间(0,+∞)上是单调减函数.(1)求函数f(x);(2)讨论F(x)=a的奇偶性3/5xOyayxbyxcyx幂依次减小幂函数图象及其性质四、比较大小1、比较下列各组中两个数的大小:(1),;(2)0.71.5,0.61.5;(3),.练习:(1)11221.5,1.7(2)33(1.2),(1.25)(3)1125.25,5.26,5.26(4)30.530.5,3,log0.52、已知点(22),在幂函数()fx的图象上,点124,,在幂函数()gx的图象上.问当x为何值时有:(1)()()fxgx;(2)()()fxgx;(3)()()fxgx.综合训练1.在函数中,幂函数的个数为()A.0B.1C.2D.32、幂函数的图象都经过点()A.(1,1)B.(0,1)C.(0,0)D.(1,0)3、幂函数的定义域为()A.(0,+)B.[0,+)C.RD.(-,0)U(0,+)4.若幂函数在上是增函数,则()A.>0B.<0C.=0D.不能确定6.若幂函数在(0,+∞)上是减函数,则()A.>1B.<1C.=lD.不能确定9、若四个幂函数y=,y=,y=,y=在同一坐标系中的图象如右图,则a、b、c、d的大小关系是()A、d>c>b>aB、a>b>c>dC、d>c>a>bD、a>b>d>c10、当x∈(1,+∞)时,函数)y=的图象恒在直线y=x的下方,则a的取值范围是A、a<1B、0<a<1C、a>0D、a<011、下面六个幂函数的图象如图所示,试建立函数与图象之间的对应关系.4/5xOyayxbyxcyx幂函数图象及其性质(A)(B)(C)(D)(E)(F)指数函数、对数函数、幂函数综合小练习1、函数的定义域为()A.(1,4)B.(-∞,1)∪(4,+∞)C.[1,4)D.(-∞,1]∪(4,+∞)2、以下四个数中的最大者是()(A)(ln2)2(B)ln(ln2)(C)ln2(D)ln23、设f(x)=则不等式f(x)>2的解集为()(A)(1,2)(3,+∞)(B)(,+∞)(C)(1,2)(,+∞)(D)...