简单的三角恒等变换二VIP免费

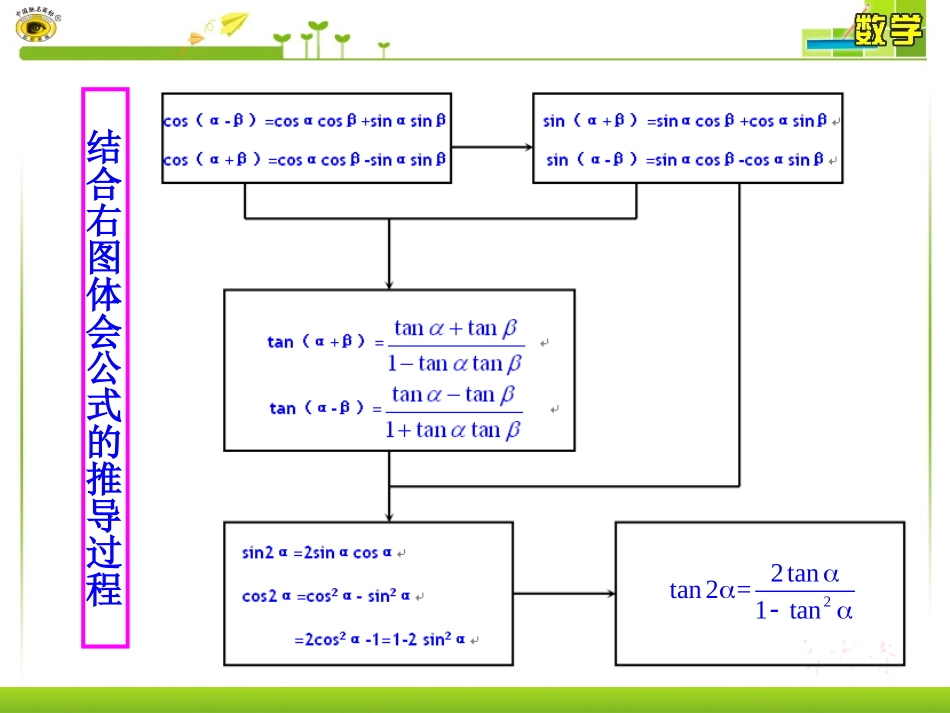
3.2简单的三角恒等变换（二）3.2简单的三角恒等变换（二）1.通过三角恒等变换，形如的函数转化为的函数；(重点）sincosaxbxsin()yAx2.灵活利用公式，通过三角恒等变换，解决函数的最值、周期、单调性等问题；(重点、难点)3.灵活运用三角公式解决一些实际问题．结合右图体会公式的推导过程22tantan2=1tan你能把下列各式化为一个角的三角函数形式吗?31sincos;22(1)sincos;(2)cossinsincossin();666222(sincos)2(cossinsincos)22442sin();4sincosaxbx(3)？2222222222222222cos,sinsincos(sincos)cossinsincossincoscossinsin.令abababaxbxababxxabababxxabxxabxsincos的变形及应用axbxsincosaxbx(3)能化成一个角的三角函数值吗？例1.求函数的周期，最大值和最小值.sin3cosyxx分析：利用三角恒等变换，先把函数式化简，再求相应的值.sin3cos132(sincos)22yxxxx解：2(sincoscossin)332sin().3xxxT2周期，最大值为2，最小值为-2.通过三角恒等变换，我们把形如的函数转化为形如的函数，从而使问题得到简化.sincosyaxbxyAsin(x)22.()cos2sin,().fxxxfx例已知函数求的单调增区间1cos211()cos2cos2.222xfxxx解：+2k2x2k,kZf(x)kxk,kZ.2当时，为增函数，即f(x)k,k(kZ).2函数的单调增区间为三角变换在化简，证明中的应用.cos10tan103.sin50例3.化简sin10cos103cos10sin50sin103cos10cos10cos10sin50解：原式（）（）13sin10cos10222sin50sin(1060)sin(50)222.sin50sin50三角恒等变换过程与方法，实际上是对三角函数式中的角、名、形的变换.（1）找差异：角、名、形的差别；（2）建立联系：角的和差关系、倍半关系等，名、形之间可以用哪个公式联系起来；（3）变公式：在实际变换过程中，往往需要将公式加以变形后正用或逆用公式，如升、降幂公式，cosα=cosβcos（α-β）-sinβsin（α-β），1=sin2α+cos2α，1tan301tan30=tan45tan301tan45tan30=tan（45°+30°）等。提升总结：常见的三角变形技巧有①切割化弦；②“1”的变用；③统一角度，统一函数，统一形式等等．三角变换在实际问题中的应用例4.如图，已知OPQ是半径为1，圆心角为的扇形，C是扇形弧上的动点，ABCD是扇形的内接矩形，记，问当角取何值时，矩形ABCD的面积最大？并求出这个最大面积.3COP分析：（1）找出与之间的函数关系；S（2）由得出的函数关系求S的最大值.OABPCDQRtOBCOBcos,BCsin.DARtOADtan603.OAo解在中，在中，：333OADABCsin,3333ABOBOAcossin.32ABCDS,3SABBC(cossin)sin33sincossin3设矩形的面积为则13sin2(1cos2)261313(sin2cos2)226313sin(2).66350,2.36662+==626133S=.6633=ABCD.66最大由得当，即时，因此,当时，矩形的面积最大，最大面积为221.(2012()cos23sincossin2fxxxxx日照高一检测)函数的最小正周期是（）.A.B.C.2D.4()3sin2cos22sin(2).62.2fxxxxT解：B22.ysinx23sinxcosx3cosx2(,).632求函数在区间上的值域1cos21cos23sin232223sin2cos242sin(2)4.6xxyxxxx解：=2cos10sin203..sin70求值：2cos(3020)sin20cos202(cos30cos20sin30sin20)sin20cos203cos203.cos20解：原式4.已知半径为1的半圆，PQRS是半圆的内接矩形，如图，P点在什么位置时，矩形的面积最大，并求最大面积的值．PQRSO分析：连接OP,设用角表示面积.,POSPQRSOPOS,OSOPcoscos,PSOPsinsin,解:连接OP,设则PORSs2OSPS2sincossin2.=s1.4矩形的面积为当时，最大，最大值为1.yasinxbcosxyAsin(x);2.形如的函数化成形式求解,体现化归思想用函数法求平面图形面积的最大或最小值，常以某个变化的角作为自变量，再将面积表示为这个角的函数，转化为三角函数的最值问题.不要对一切人都以不信任的眼光看待,但要谨慎而坚定。——德谟克里特