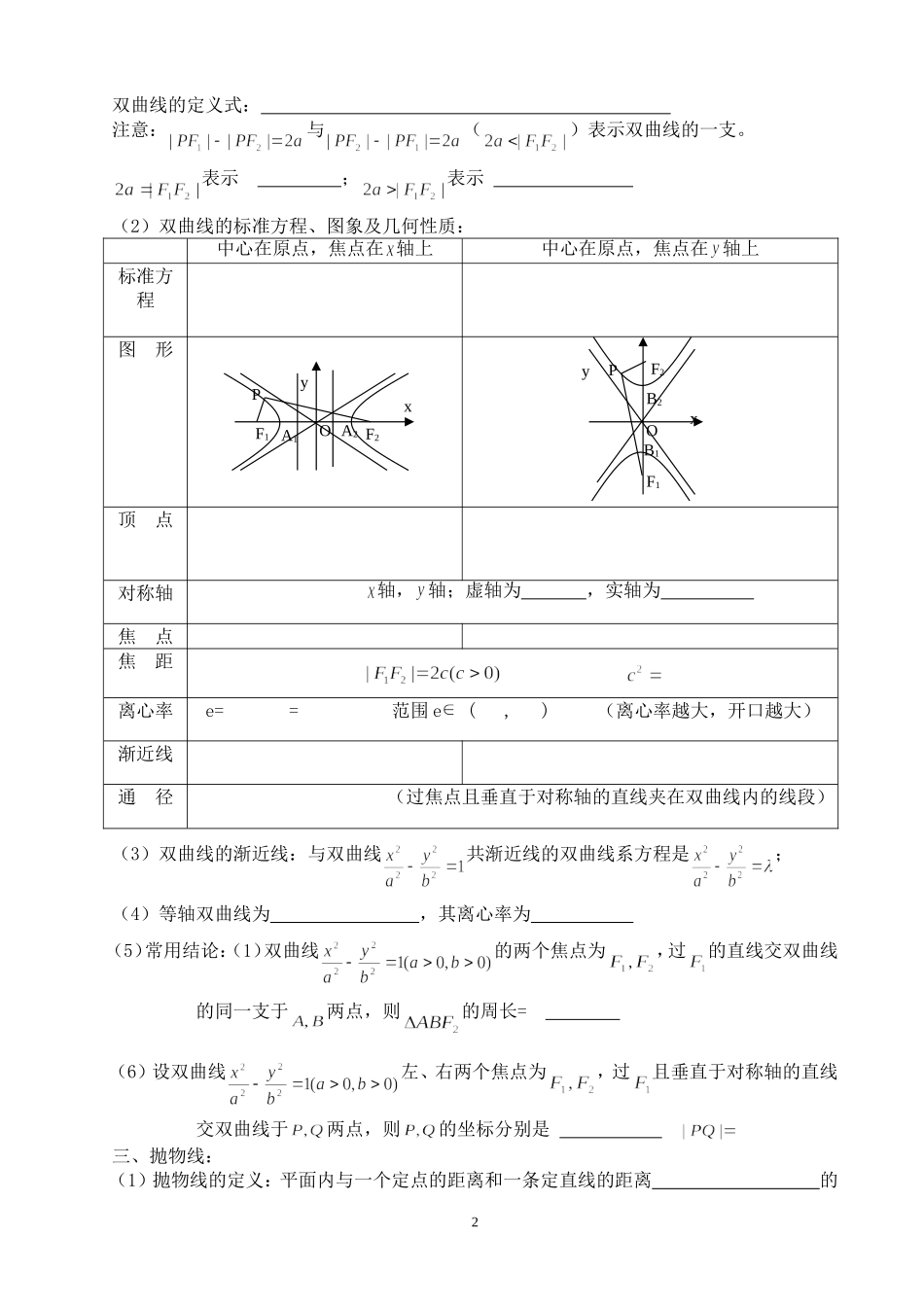
《圆锥曲线》知识点小结班级姓名一、椭圆:1,椭圆的定义:平面内与两个定点的常数(大于)的点的轨迹。其中:两个定点叫做椭圆的焦点,焦点间的距离叫做焦距。,椭圆的定义式:注意:表示;表示;;2,椭圆的标准方程、图象及几何性质:中心在原点,焦点在轴上中心在原点,焦点在轴上标准方程图形顶点对称轴轴,轴;短轴为,长轴为焦点焦距离心率=范围通径(过焦点且垂直于对称轴的直线夹在椭圆内的线段)3.(1)椭圆的两个焦点为,过的直线交椭圆于两点,则的周长=(2)设椭圆左、右两个焦点为,过且垂直于对称轴的直线交椭圆于两点,则的坐标分别是二、双曲线:(1)双曲线的定义:平面内与两个定点的等于常数(小于)的点的轨迹。其中:两个定点叫做双曲线的,焦点间的距离叫做。xOF1F2PyA2A1B1B2xOF1F2PyA2B2B11A1双曲线的定义式:注意:与()表示双曲线的一支。表示;表示(2)双曲线的标准方程、图象及几何性质:中心在原点,焦点在轴上中心在原点,焦点在轴上标准方程图形顶点对称轴轴,轴;虚轴为,实轴为焦点焦距离心率e==范围e(,)(离心率越大,开口越大)渐近线通径(过焦点且垂直于对称轴的直线夹在双曲线内的线段)(3)双曲线的渐近线:与双曲线共渐近线的双曲线系方程是;(4)等轴双曲线为,其离心率为(5)常用结论:(1)双曲线的两个焦点为,过的直线交双曲线的同一支于两点,则的周长=(6)设双曲线左、右两个焦点为,过且垂直于对称轴的直线交双曲线于两点,则的坐标分别是三、抛物线:(1)抛物线的定义:平面内与一个定点的距离和一条定直线的距离的xOF1F2PyA2A1xOF1PB2B1F22y点的轨迹。其中:定点为抛物线的焦点,定直线叫做准线。(2)抛物线的标准方程、图象及几何性质:3、弦长公式:习题:1.已知椭圆长半轴与短半轴之比是5:3,焦距是8,焦点在x轴上,则此椭圆的标准方程是()(A)+=1(B)+=1(C)+=1(D)+=12.以椭圆短轴为直径的圆经过此椭圆的焦点,则椭圆的离心率是()(A)(B)(C)(D)3.已知椭圆的对称轴是坐标轴,离心率e=,长轴长为6,那么椭圆的方程是()。(A)+=1(B)+=1或+=1焦点在轴上,开口向右焦点在轴上,开口向左焦点在轴上,开口向上焦点在轴上,开口向下标准方程图形顶点对称轴轴轴焦点离心率准线通径(过焦点且垂直于对称轴的直线夹在抛物线内的线段)焦半径焦点弦焦准距3(C)+=1(D)+=1或+=14.已知两点A(-3,0)与B(3,0),若|PA|+|PB|=10,那么P点的轨迹方程是。5.平面内有两个定点F1(-5,0)和F2(5,0),动点P满足条件|PF1|-|PF2|=6,则动点P的轨迹方程是()。(A)-=1(x≤-4)(B)-=1(x≤-3)(C)-=1(x>≥4)(D)-=1(x≥3)6双曲线-=1的渐近线方程是()(A)±=0(B)±=0(C)±=0(D)±=07.设双曲线(b>a>0)的半焦距为c,直线l过(a,0)、(0,b)两点,已知原点到直线l的距离是c,则双曲线的离心率是()(A)2(B)(C)(D)8.双曲线-=1的离心率是。9,已知方程+=1表示双曲线,则k的取值范围是。10.双曲线的两个顶点三等分两个焦点间的线段,则离心率e=。11.抛物线y2=8x的准线方程是()。(A)x=-2(B)x=2(C)x=-4(D)y=-212.AB是过抛物线y2=4x焦点F的弦,已知A,B两点的横坐标分别是x1和x2,且x1+x2=6则|AB|等于()(A)10(B)8(C)7(D)613.已知点(-2,3)与抛物线y2=2px(p>0)的焦点的距离是5,则抛物线的方程是。14.抛物线x2=4y上有一点Q到焦点的距离为3,那么Q点的纵坐标是()。(A)-2(B)2(C)4(D)115.抛物线y=4x2的准线方程是()。(A)x=-1(B)y=-1(C)x=-(D)y=-4