第三章 分层随机抽样VIP免费

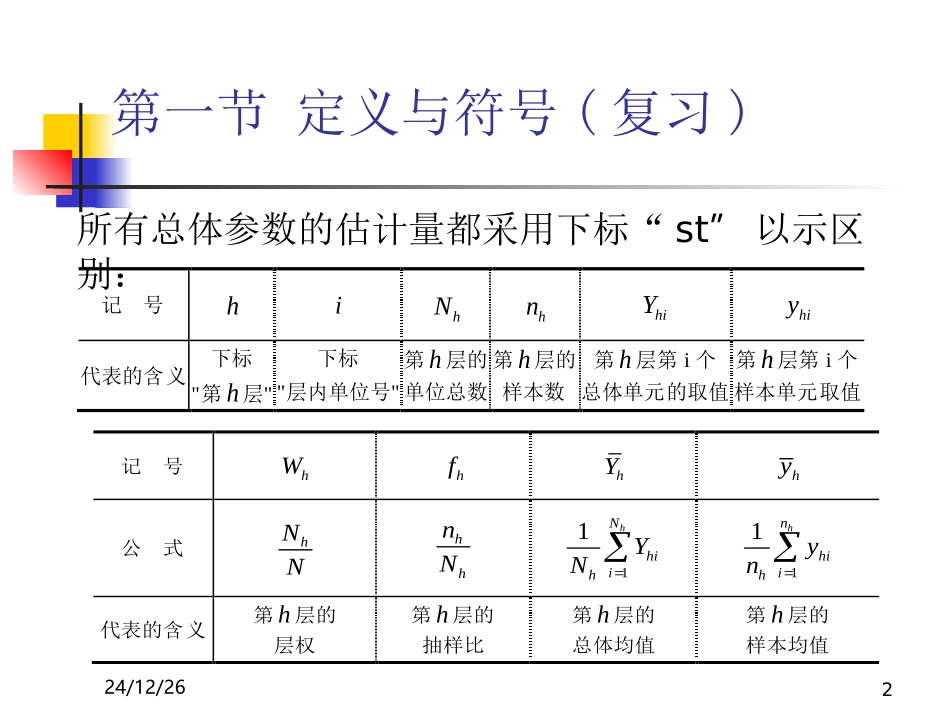
24/12/261第三章分层随机抽样第一节定义与符号第二节简单估计量及其性质第五节各层样本量的分配第六节总样本量的确定第一节定义与符号(复习)24/12/262所有总体参数的估计量都采用下标“st”以示区别：记号hihNhnhiYhiy代表的含义下标"第h层"下标"层内单位号"第h层的单位总数第h层的样本数第h层第i个总体单元的取值第h层第i个样本单元取值记号hWhfhYhy公式hNNhhnN11hNhiihYN11hnhiihyn代表的含义第h层的层权第h层的抽样比第h层的总体均值第h层的样本均值24/12/263记号hYhy2hS2hs公式1hNhihhiYNY1hnhihhiyny21()1hNhihihYYN21()1hnhihihyyn代表的含义第h层的总体总量第h层的样本总量第h层的总体方差第h层的样本方差24/12/264第二节简单估计量及其性质总体均值的简单估计对于分层随机抽样，总体均值的简单估计量为111.LLsthhhhhhyWyNyNY,stEyy2211.LhststhhhhfVyvyWsn的无偏估计：Y的1-置信区间：22(),().ststststyzvyyzvy21()LsthhhVyWVy2211.LhhhhhfWSn24/12/265第二节简单估计量及其性质总体总量的简单估计对于分层随机抽样，总体总量的简单估计量为ˆststYNyY2211ˆˆ(),.LhststhhhhfEYYVYNSn2211ˆˆ.LhststhhhhfVYvYNsn的无偏估计：1LhhhNWy1LhhhNNyN1LhhhNyY的1-置信区间：22ˆˆˆˆ(),().ststststYzvYYzvY24/12/266解：(1)试估计该小区居民购买彩票的平均支出，并给出估计的标准差。111.2,y根据表中数据，每层样本均值为：3.3习题下表是每个新村10个居民户购买彩票所花费的金额(元)：1234567891012561010202010010302024202035105004050102020316802003030新村居民户数50400300(1)225.5,y320.y每层单位总数为：123256,420,168.NNN844N单位总数.每层层权为：110.3033,NWN220.4976,NWN330.1991.NWN该小区居民购买彩票的平均支出的估计值为：31sthhhyWy20.0678.24/12/267解：(1)试估计该小区居民购买彩票的平均支出，并给出估计的标准差。2194.4,s根据表中数据，每层样本方差为：3.3习题下表是每个新村10个居民户购买彩票所花费的金额(元)：1234567891012561010202010010302024202035105004050102020316802003030新村居民户数50400300(1)22302.5,s23355.556.s每层样本数为：12310.nnn每层抽样比为：1110.03901,nfN2220.0238,nfN3330.0595.nfN估计的方差为：2211LhsthhhhfvyWsn估计的标准差为：ststsyvy9.4731.3.08.8第二节简单估计量及其性质总体比例的简单估计总体比例P的估计为：估计量的性质pWpsthhhL1对于一般的分层抽样，如果是的无偏估计（），则是的无偏估计。的方差为：hphPhL12,,,pstPpstVpWVpsthhhL219P推论3.2对于分层随机抽样，总体比例的简单估计1LsthhhpWp有如下性质:(1)()stEpP211(2)(),1LhhhhsthhhhfNPQVpWnN1.hhQP其中hN说明：当较大时，221111(3)()11LLhhhhhsthhhhhhhhhfnpqfvpWWpqnnn211(),LhsthhhhhfVpWPQn()stVp是的一个无偏估计。10例3.2在例3.1的调查中，同时调查了居民户拥有家庭电脑的情况，获得如下数据（单位：台），要估计该地区居民拥有家庭电脑的比例及估计的标准差。层居民户总数样本户拥有家庭电脑情况12345678910120000010001002400010000001037501100001010415001000000000112.01p2.02p4.03p1.04phWhf1111110.01691pqvpfn2222210.01731pqvpfn3333310.02631pqvpfn4444410.00991pqvpfn41411hhhhhhstpNNpWp12000.24000.27500.415000.128500.241221hhhstpvNNpv2222212000.01694000.01737500.026315000.009928500.0050.07ststspvp解：由上表可得，根据前面对各层层权及抽样比的计算结果，可得各层估计量的方差：因...