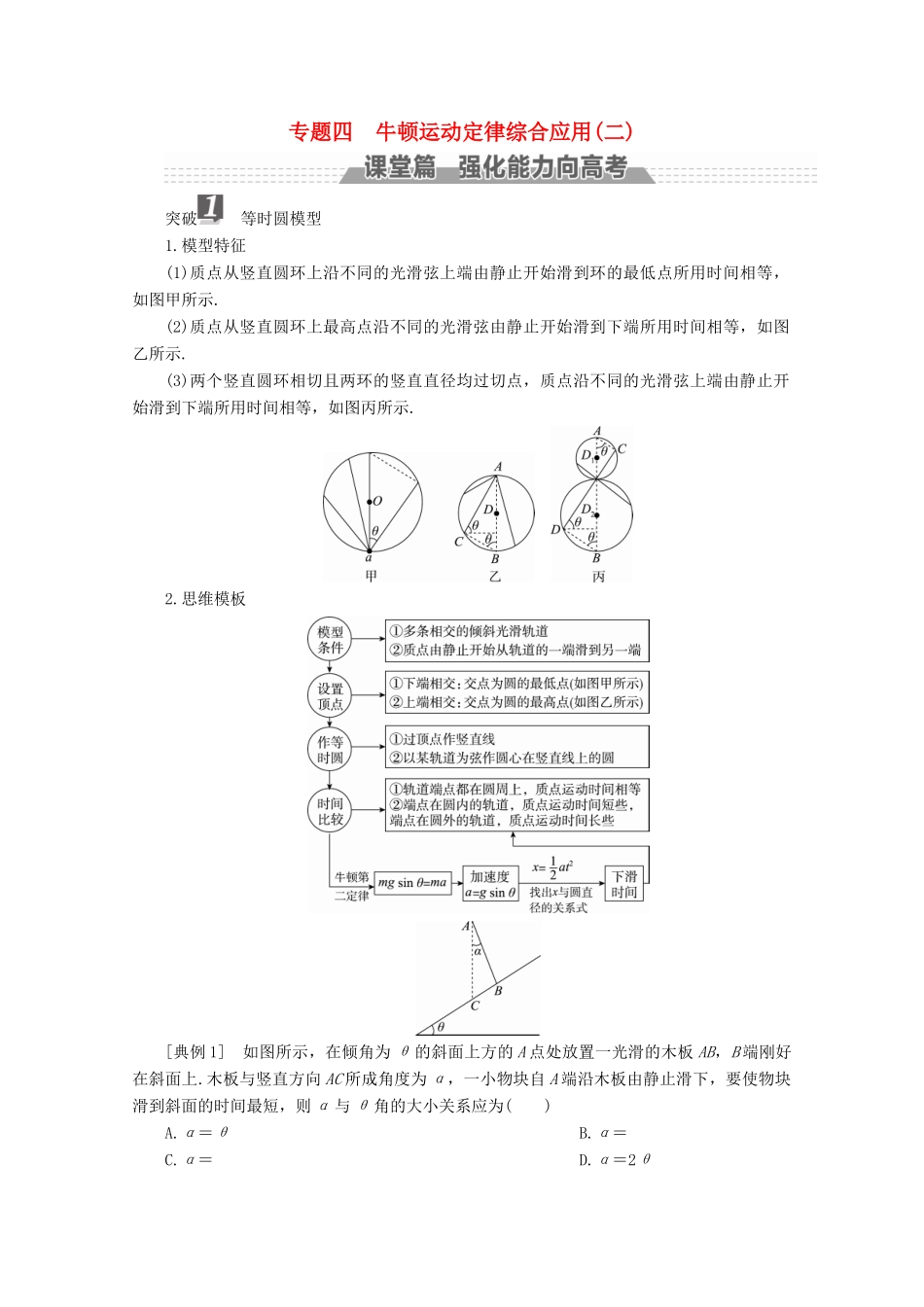
专题四牛顿运动定律综合应用(二)突破等时圆模型1.模型特征(1)质点从竖直圆环上沿不同的光滑弦上端由静止开始滑到环的最低点所用时间相等,如图甲所示.(2)质点从竖直圆环上最高点沿不同的光滑弦由静止开始滑到下端所用时间相等,如图乙所示.(3)两个竖直圆环相切且两环的竖直直径均过切点,质点沿不同的光滑弦上端由静止开始滑到下端所用时间相等,如图丙所示.2.思维模板[典例1]如图所示,在倾角为θ的斜面上方的A点处放置一光滑的木板AB,B端刚好在斜面上.木板与竖直方向AC所成角度为α,一小物块自A端沿木板由静止滑下,要使物块滑到斜面的时间最短,则α与θ角的大小关系应为()A.α=θB.α=C.α=D.α=2θ[解题指导]在AC上选取一点O,使OA=OB,以O为圆心,OA为半径作圆,即可构造等时圆模型.[解析]如图所示,在竖直线AC上选取一点O为圆心,以适当的长度为半径画圆,使该圆过A点,且与斜面相切于B点.由等时圆知识可知,由A沿斜面滑到B所用时间比由A到达斜面上其他各点所用时间都短.而∠COB=θ,则α=.[答案]B[变式1](2017·东北三省三校第一次联考)如图所示,位于竖直平面内的固定光滑圆环轨道与水平面相切于M点,与竖直墙相切于A点.竖直墙上另一点B与M的连线和水平面的夹角为60°,C是圆环轨道的圆心.已知在同一时刻a、b两球分别由A、B两点从静止开始沿光滑倾斜直轨道AM、BM运动到M点;c球由C点自由下落到M点.则()A.a球最先到达M点B.b球最先到达M点C.c球最先到达M点D.b球和c球都可能最先到达M点答案:C解析:如图所示,令圆环半径为R,则c球由C点自由下落到M点用时满足R=gt,所以tc=;对于a球令AM与水平面成θ角,则a球下滑到M用时满足AM=2Rsinθ=gsinθt,即ta=2;同理b球从B点下滑到M点用时也满足tb=2(r为过B、M且与水平面相切于M点的竖直圆的半径,r>R).综上所述可得tb>ta>tc.突破传送带模型考向1水平传送带模型情景图示滑块可能的运动情况情景1(1)可能一直加速(2)可能先加速后匀速情景2(1)v0=v时,一直匀速(2)v0>v时,可能一直减速,也可能先减速再匀速(3)v0v时,返回时速度为v;当v0