高二数学斜线与平面三垂线定理教案人教版VIP免费

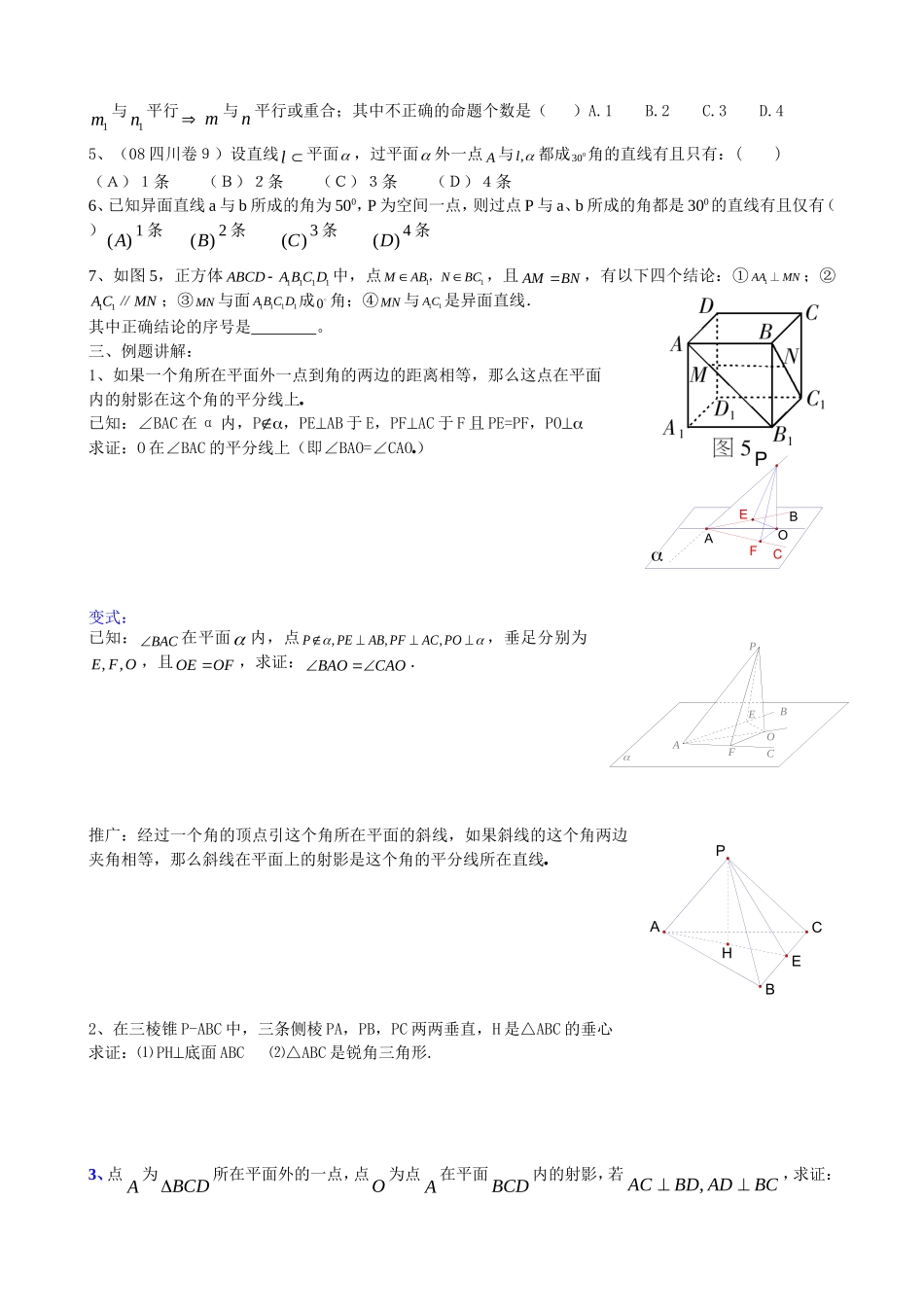
斜线与平面三垂线定理一、知识要点：1、斜线在平面内的射影①点在平面的射影，垂线段：②平面的斜线，斜足，斜线段的定义③斜线在平面内的射影，斜线段在平面的射影。2、射影定理从平面外一点向这个平面所引的垂线段和斜线段中：①射影相等的两条斜线段相等，射影较长的斜线段也较长；②相等的斜线段的射影也相等，较长的斜线段的射影也较长；③垂线段比任何一条斜线段都短。3、直线和平面所成的角，范围为2,0①斜线和平面所成的角：平面的斜线和它在这个平面内的射影所处的锐角。范围为：2,0②若直线和平面垂直，则线面所成的角为直角。③若直线和平面平行或在平面内，则线面所成的角为0的角。4、①斜线和平面所成的角，是这条斜线和这个平面内经过斜足的直线所成的一切角中的最小角。②斜线和平面所成的角，是这条斜线和这个平面内的直线所成的一切角中的最小角。5、三垂线定理在平面内的一条直线，如果它和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直。已知：,POPA分别是平面的垂线和斜线，OA是PA在平面内的射影，a，且aOA求证：aPA；说明：定理的实质是判定平面内的一条直线和平面的一条斜线的垂直关系。6、三垂线定理的逆定理：在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它也和这条斜线的射影垂直奎屯王新敞新疆注意：⑴三垂线指PA，PO，AO都垂直α内的直线a奎屯王新敞新疆其实质是：斜线和平面内一条直线垂直的判定和性质定理奎屯王新敞新疆⑵要考虑a的位置，并注意两定理交替使用奎屯王新敞新疆7、①如果一个角所在平面外一点到角的两边的距离相等，那么这点在平面内的射影在这个角的平分线上奎屯王新敞新疆②如果经过一个角的顶点引这个角所在平面的斜线，如果斜线的这个角两边夹角相等，那么斜线在平面上的射影是这个角的平分线所在直线奎屯王新敞新疆二、高考题集1、（2006年全国卷II）如图，平面α⊥平面β，A∈α，B∈β，AB与两平面α、β所成的角分别为和，过A、B分别作两平面交线的垂线，垂足为A′、B′，则AB∶A′B′＝()（A）2∶1（B）3∶1（C）3∶2（D）4∶32、（2006年四川卷）在三棱锥0ABC中，三条棱,,OAOBOC两两互相垂直，且,OAOBOCM是AB边的中点，则OM与平面ABC所成角的大小是_______（用反三角函数表示）3、（2006年重庆理）对于任意直线l与平面，在平面内必有直线m，使m与l（）.（A）平行（B）相交（C）垂直（D）互为异面直线4、（07湖北•理•4题）平面外有两条直线m和n，如果m和n在平面内的射影分别是1m和1n，给出下列四个命题：①1m⊥1nm⊥n；②m⊥n1m⊥1n；③1m与1n相交m与n相交或重合；④αβABA′B′aPOA1m与1n平行m与n平行或重合；其中不正确的命题个数是（）A.1B.2C.3D.45、（08四川卷９）设直线l平面，过平面外一点A与,l都成030角的直线有且只有：()（Ａ）１条（Ｂ）２条（Ｃ）３条（Ｄ）４条6、已知异面直线a与b所成的角为500，P为空间一点，则过点P与a、b所成的角都是300的直线有且仅有（）()A1条()B2条()C3条()D4条7、如图5，正方体1111ABCDABCD中，点11MABNBC，，且AMBN，有以下四个结论：①1AAMN⊥；②11ACMN∥；③MN与面1111ABCD成0角；④MN与11AC是异面直线．其中正确结论的序号是。三、例题讲解：1、如果一个角所在平面外一点到角的两边的距离相等，那么这点在平面内的射影在这个角的平分线上奎屯王新敞新疆已知：∠BAC在α内，P，PEAB于E，PFAC于F且PE=PF，PO求证：O在∠BAC的平分线上（即∠BAO=∠CAO奎屯王新敞新疆）变式：已知：BAC在平面内，点,,,PPEABPFACPO，垂足分别为OFE,,，且OFOE，求证：BAOCAO．推广：经过一个角的顶点引这个角所在平面的斜线，如果斜线的这个角两边夹角相等，那么斜线在平面上的射影是这个角的平分线所在直线奎屯王新敞新疆2、在三棱锥P-ABC中，三条侧棱PA，PB，PC两两垂直，H是△ABC的垂心求证：⑴PH底面ABC⑵△ABC是锐角三角形.3、点A为BCD所在平面外的一点，点O为点A在平面BCD内的射影，若,ACBDADBC，求证：CFEPOABPOEFCBAABCP...