高一数学：6.2 正切函数的图像与性质教案（1）沪教版VIP免费

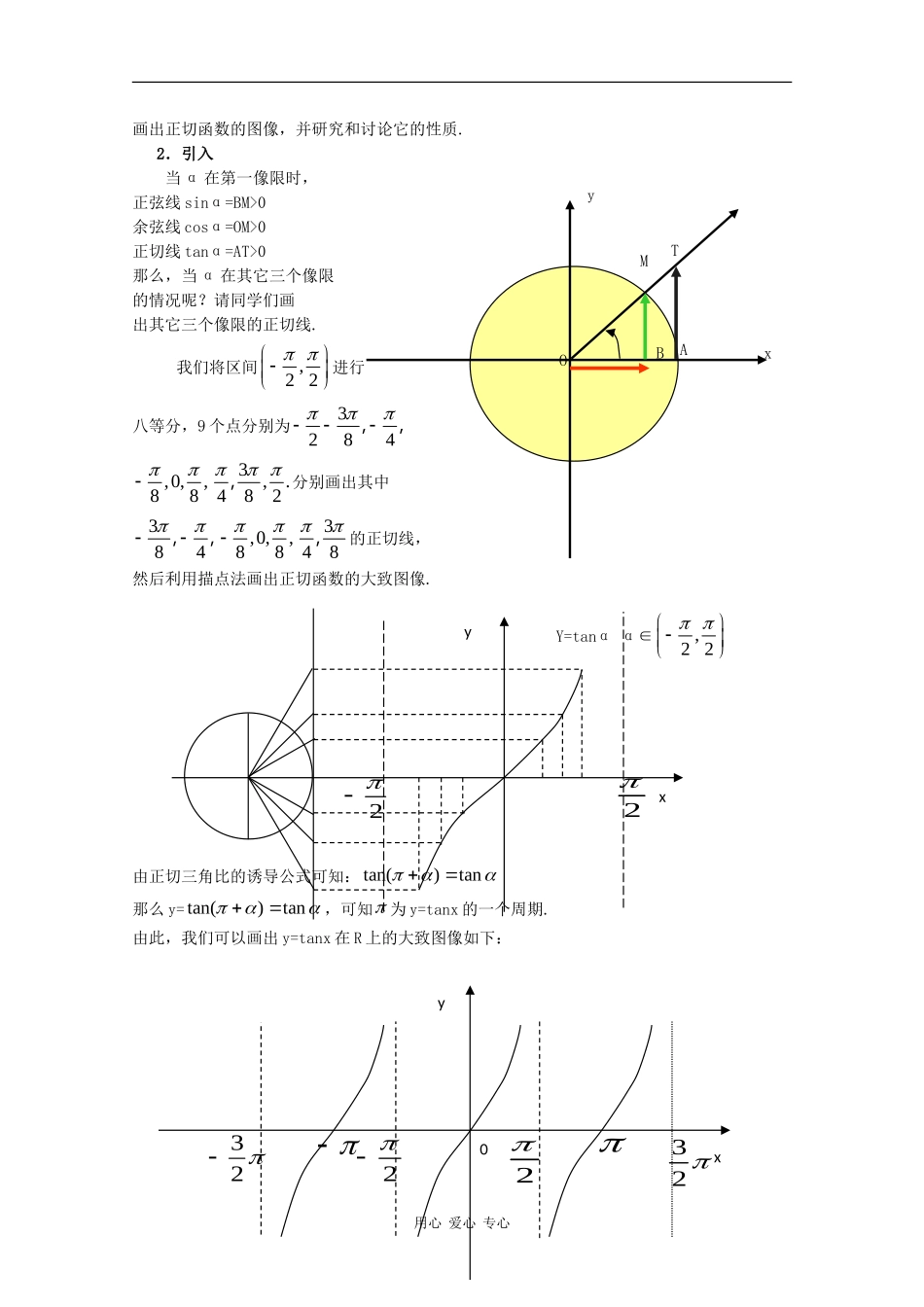
6.26.2正切函数的图像与性质（正切函数的图像与性质（11））一、教学内容分析本节内容是学生在学习了正弦、余弦函数图像和基本性质以后的知识，学生已经掌握了三角函数线的画法，并且对三角函数性质的讨论方法已经有了一个比较清晰的认识.因此通过正切函数的图像来认识函数的性质，并通过例题来巩固对性质的掌握是学习“正切函数的图像与性质”的一条主线.二、教学目标设计1.理解利用正切线作出的正切函数图像.2.通过观察正切函数图像了解与感悟正切函数的性质.3.通过练习与训练体验并初步掌握正切函数的基本性质.三、教学重点及难点利用正切线作正切函数的图像；正切函数单调性的证明以及周期性的确定.四、教学用具准备多媒体设备五、教学流程设计六、教学过程设计一、复习引入1．复习我们在前几节中学习了正弦函数线、余弦函数线以及正切函数线，我们通过正弦函数线，画出了正弦函数的图像，并研究了函数的性质.今天，我们同样按照这样的方法通过正切线来用心爱心专心利用正切线作出正切函数在上的图像利用诱导公式，画出在R上的大致图像；观察图像，探索与讨论正切函数的性质引导学生证明正切函数单调性并利用单调性解决一些实际例题；通过周期的求解，感悟求一般函数y=tan(ωx+φ)周期的方法总结提炼方法，结合图像归纳小结函数性质布置课外作业画出正切函数的图像，并研究和讨论它的性质.2．引入当α在第一像限时，正弦线sinα=BM>0余弦线cosα=OM>0正切线tanα=AT>0那么，当α在其它三个像限的情况呢？请同学们画出其它三个像限的正切线.我们将区间,22进行八等分，9个点分别为3284，，,0,,883,.482，分别画出其中384，，,0,,88348，的正切线，然后利用描点法画出正切函数的大致图像.由正切三角比的诱导公式可知：tan()tan那么y=tan()tan，可知为y=tanx的一个周期.由此，我们可以画出y=tanx在R上的大致图像如下：用心爱心专心yTMABxOY=tanαα∈,22xy222322230yx二、学习新课1.探究性质观察正切函数的图像，引导学生得正切函数的性质：1.定义域：|,2xxkkz，2.值域：R观察：当x从小于zkk2，2kx时，xtan当x从大于2kkz，2xk时，xtan.3.周期性：T4.奇偶性：xxtantan奇函数.5.单调性：在开区间,22kkkz内，函数单调递增.从图像上看出函数y=tanx的单调区间是,22kkkz，但是我们怎样从理论上去加以证明呢？考察0,2这个区间内的函数y=tanx的单调性.在0,2这个区间内任意取12xx、，且12xx，y1-y2=tanx1-tanx2=1212sinsincoscosxxxx=1212121212sincoscossinsin()coscoscoscosxxxxxxxxxx.因为1202xx，所以120.2xx则cosx1、cosx2>0用心爱心专心sin(12xx)<0,从而tanx1-tanx2<0，y10.因此1+tanx1·tanx2>0.则tanx1-tanx2<0,tanx1