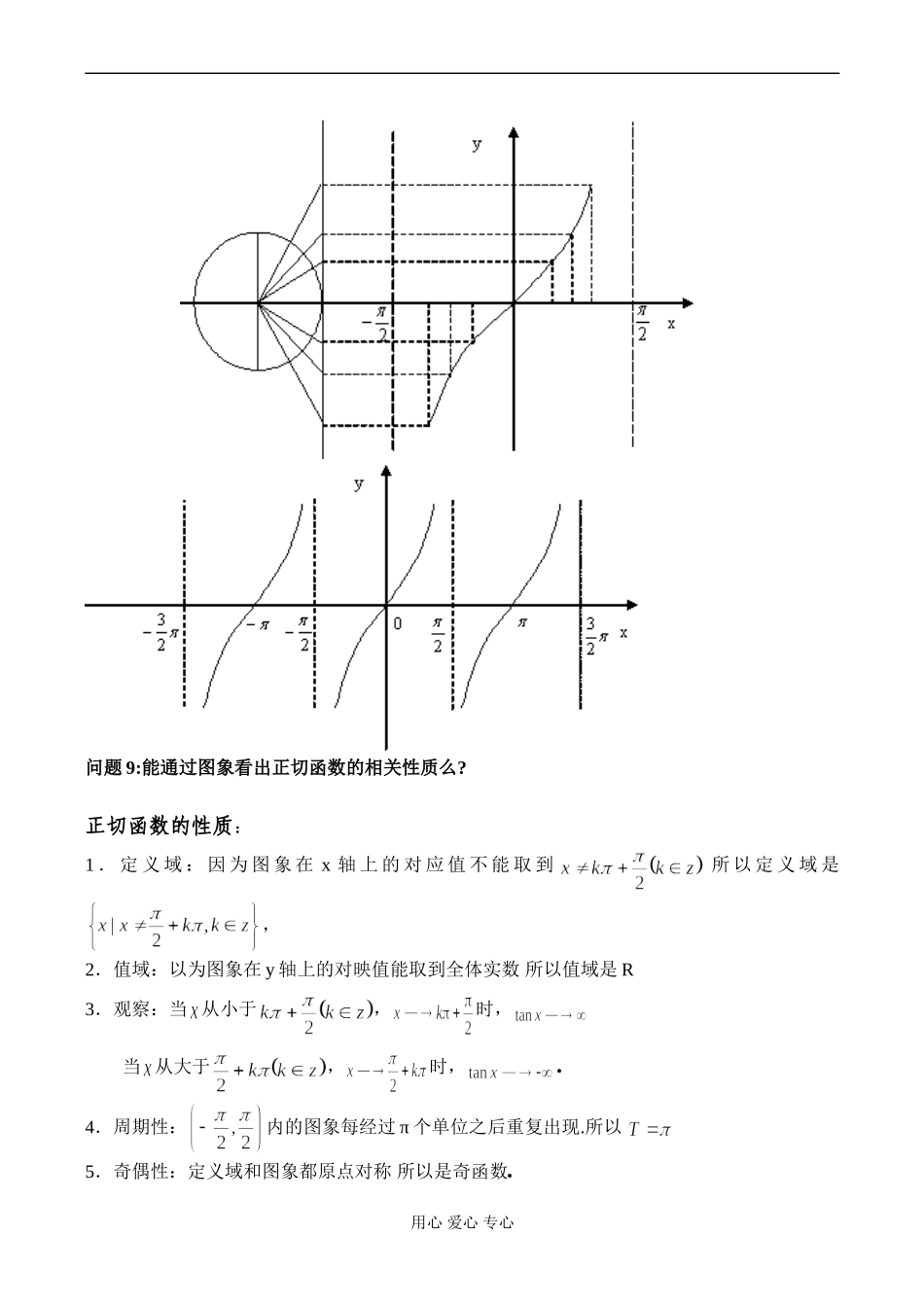
高一数学正切函数的图象和性质教学目的:1.理解并掌握作正切函数图象的方法.2.能利用正切函数的性质以及图象解决相关问题3.培养学生辨证唯物的世界观教学重点:正切图象的做法及正切函数的性质教学难点:作正切函数的图象.授课类型:新授课课时安排:1课时教学过程:一、复习引入:我们知道函数图象在解决函数性质上有很大的用处,并且图象和性质本身就有强烈的联系,我们前面学过的正弦函数和余弦函数都验证了这个理论,那么正切函数的图象有没有这样的验证关系呢?首先我们看问题1:我们是用什么方法做正弦函数图象的?利用三角函数线问题2:你知道三角函数线中正切线是怎么做的么?正切线:首先练习正切线,画出下列各角的正切线:正切线是AT.二、讲解新课:问题3:我们在研究函数和做函数图象的时候最先思考的是什么?首先考虑定义域:用心爱心专心是由正切线的定义角的终边不能落在y轴上问题4:有正切线你能看出正切函数的周期么?能,周期为能利用周期函数的定义来证明么问题5:那能看出当x在中正切值的变化规律么?当从中增大的时候,当从中减小的时候问题6:能利用函数的周期性说明正切函数在开区间中的变化规律么?当从小于,时,当从大于,时,问题7:能看出正切函数的值域么?由5.6问题中可以看出正切函数的值域是R问题8:正切函数的奇偶性:所以是奇函数下面我们利用正切线作出正切函数的图象,验证一下我们通过正切线的得到的正切函数的性质是否正确!正切函数的图象:因为每当角在y轴右侧的正切线总是与他关于原点对称的角的正切线一直所以我们可选择的区间作出它的图象奎屯王新敞新疆把上述图象向左、右扩展,得到正切函数,且的图象,称“正切曲线”用心爱心专心问题9:能通过图象看出正切函数的相关性质么?正切函数的性质:1.定义域:因为图象在x轴上的对应值不能取到所以定义域是,2.值域:以为图象在y轴上的对映值能取到全体实数所以值域是R3.观察:当从小于,时,当从大于,时,奎屯王新敞新疆4.周期性:内的图象每经过π个单位之后重复出现.所以5.奇偶性:定义域和图象都原点对称所以是奇函数奎屯王新敞新疆用心爱心专心6.单调性:由观察的到的和周期性,可以看出正切函数在开区间内,函数单调递增奎屯王新敞新疆我们可以根据正切函数和他的图象及性质,又一次验证了图象与函数性质的对应关系,希望同学们好好把握!问题10.能利用正切函数的讨论函数的性质奎屯王新敞新疆略解:定义域:值域:R奇偶性:非奇非偶函数单调性:在上是增函数奎屯王新敞新疆图象:可看作是的图象向左平移单位奎屯王新敞新疆问题11.变式训练:1.利用正切函数性质和图象比较与的大小奎屯王新敞新疆解:,,又:内单调递增,奎屯王新敞新疆2.求函数y=tan2x的定义域奎屯王新敞新疆解:由2x≠kπ+,(k∈Z)得x≠+,(k∈Z)∴y=tan2x的定义域为:{x|x∈R且x≠+,k∈Z}3.观察正切曲线写出满足下列条件的x的值的范围:tanx>0解:画出y=tanx在(-,)上的图象,不难看出在此区间上满足tanx>0的x的范围为:0<x<结合周期性,可知在x∈R,且x≠kπ+上满足的x的取值范围为(kπ,kπ+)(k∈Z)用心爱心专心三、小结本节课我们研究了正切函数的图象和性质,并且验证了函数图象和性质的紧密联系,并能在解题中应用.希望能熟练掌握.四、作业:P452.3.4.6用心爱心专心