高一数学 一元一次不等式解法1精品教案 新人教A版VIP免费

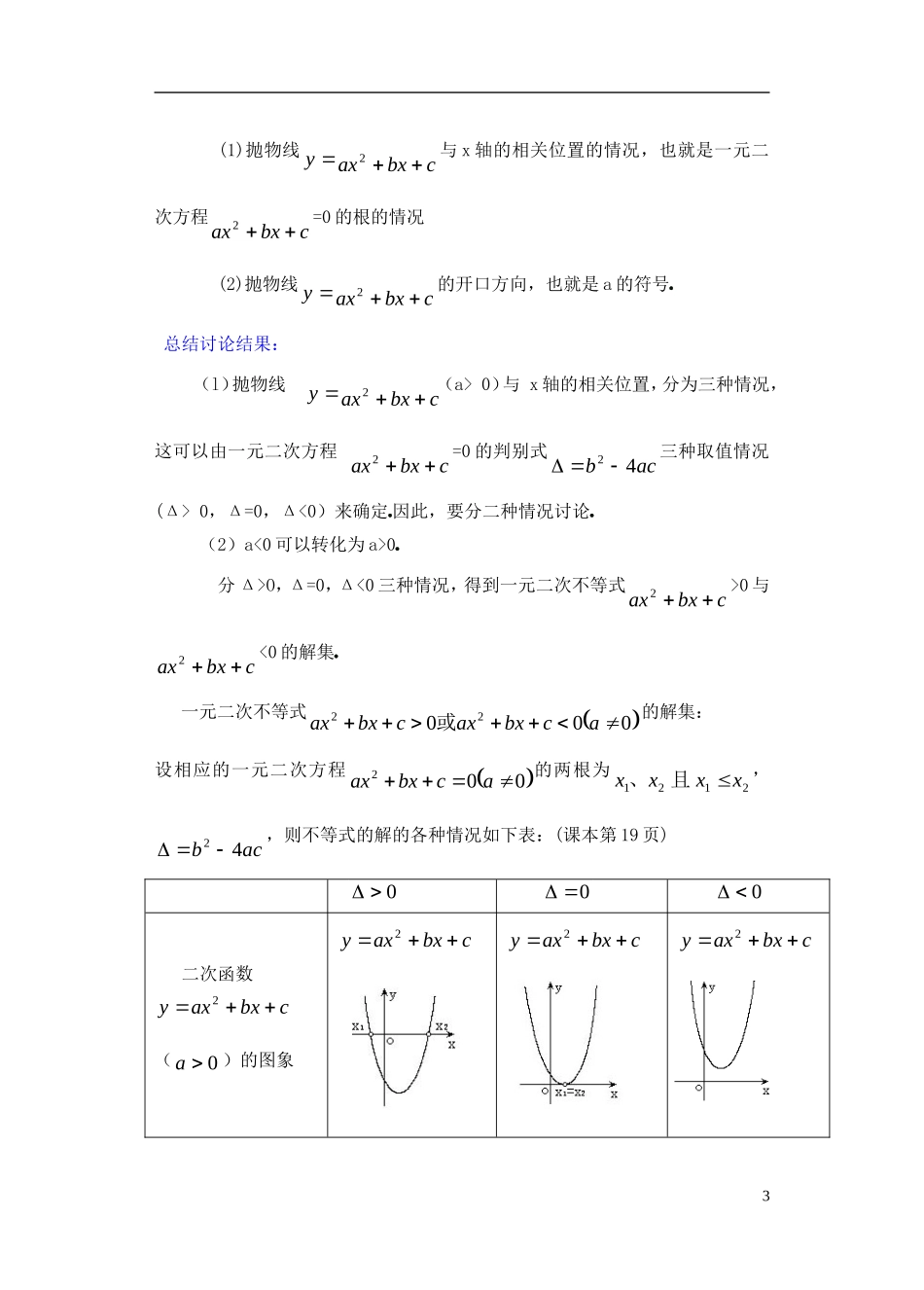
课题：1.5一元二次不等式（一）教学目的：1．理解一元二次方程、一元二次不等式与二次函数的关系，掌握图象法解一元二次不等式的方法；2．培养数形结合的能力，培养分类讨论的思想方法，培养抽象概括能力和逻辑思维能力；3．激发学习数学的热情，培养勇于探索的精神，勇于创新精神，同时体会事物之间普遍联系的辩证思想奎屯王新敞新疆教学重点：图象法解一元二次不等式奎屯王新敞新疆教学难点：字母系数的讨论；一元二次方程一元二次不等式与二次函数的关系奎屯王新敞新疆授课类型：新授课课时安排：1课时教具：多媒体、实物投影仪内容分析：1．本小节首先对照学生已经了解的一元一次方程、一元一次不等式与一次函数的关系，利用二次函数的图象，找出一元二次方程、一元二次不等式与二次函数的关系，进而得到利用二次函数图象求解一元二次不等式的方法奎屯王新敞新疆然后，说明一元二次不等式可以转化为一元一次不等式组，由此又引出了简单的分式不等式的解法奎屯王新敞新疆2．本节课学习一元二次不等式的解法，这是这小节的重点，关键是弄清一元二次方程、一元二次不等式与二次函数的关系奎屯王新敞新疆教学过程：一、复习引入：1．当x取什么值的时候，3x－15的值（l）等于0；（2）大于0；（3）小于0奎屯王新敞新疆（这是初中作过的题目）2．你可以用几种方法求解上题？3.一次函数、一元一次方程和一元一次不等式的关系(课本第17页的例子)4．像3x－15＞0(或＜0）这样的不等式，常用的有两种解法奎屯王新敞新疆(1)图象解法：利用一次函数y＝3x－15的图象求解奎屯王新敞新疆注：①直线与x轴交点的横坐标，就是对应的一元一次方程的根奎屯王新敞新疆②图象在x轴上面的部分表示3x－15＞0奎屯王新敞新疆(2)代数解法：用不等式的三条基本性质直接求解奎屯王新敞新疆1注这个方法也是对比一元一次方程的解法得到的奎屯王新敞新疆二、讲解新课：画出函数y62xx的图象，利用图象回答：（1）方程62xx＝0的解是什么；（2）x取什么值时，函数值大于0；（3）x取什么值时，函数值小于0奎屯王新敞新疆（这也是初中作过的题目）结合二次函数y62xx的对应值表与图象（表、图略），可以得出，方程62xx＝0的解是x＝－2，或x＝3；当x<-2，或x>3时，y>0，即62xx>0；当-20的解集是{x|x<-2,或x>3}；一元二次不等式62xx<0的解集是{x|-20与cbxax2<0的解集呢？组织讨论：从上面的例子出发，综合学生的意见，可以归纳出确定一元二次不等式的解集，关键要考虑以下两点：2(1)抛物线ycbxax2与x轴的相关位置的情况，也就是一元二次方程cbxax2=0的根的情况(2)抛物线ycbxax2的开口方向，也就是a的符号奎屯王新敞新疆总结讨论结果：（l）抛物线ycbxax2（a>0）与x轴的相关位置，分为三种情况，这可以由一元二次方程cbxax2=0的判别式acb42三种取值情况(Δ>0，Δ=0，Δ<0）来确定奎屯王新敞新疆因此，要分二种情况讨论奎屯王新敞新疆（2）a<0可以转化为a>0奎屯王新敞新疆分Δ>O，Δ=0，Δ<0三种情况，得到一元二次不等式cbxax2>0与cbxax2<0的解集奎屯王新敞新疆一元二次不等式00022acbxaxcbxax或的解集：设相应的一元二次方程002acbxax的两根为2121xxxx且、，acb42，则不等式的解的各种情况如下表：(课本第19页)000二次函数cbxaxy2（0a）的图象cbxaxy2cbxaxy2cbxaxy23一元二次方程的根002acbxax有两相异实根)(,2121xxxx有两相等实根abxx221无实根的解集)0(02acbxax21xxxxx或abxx2R的解集)0(02acbxax21xxxx三、讲解范例：例1(课本第19页)解不等式02632xx解：作出函数2632xxy的图像因为331,3310263,0212xxxx的解是方程....