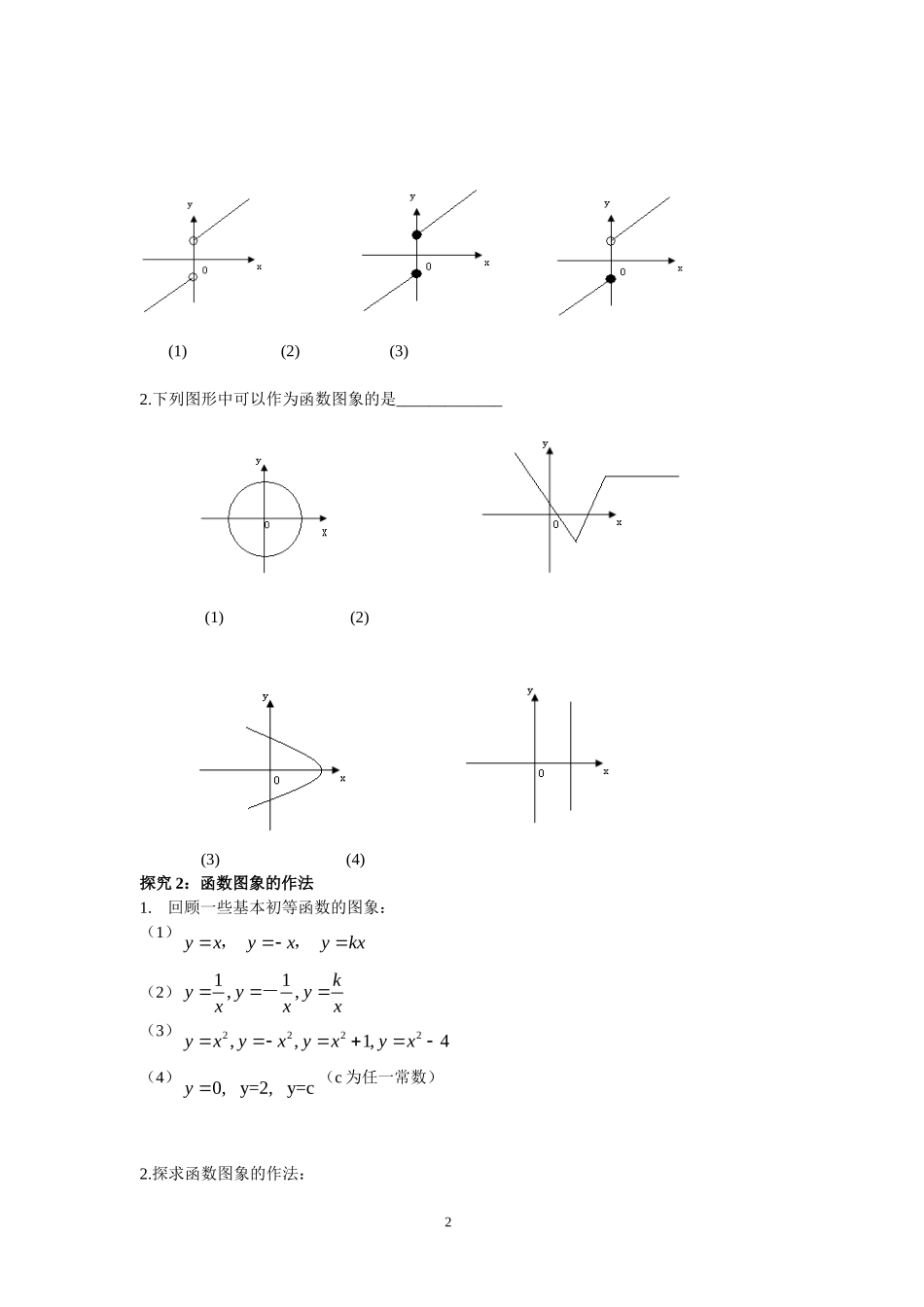
函数的图象教学目标:1.理解函数图象的定义,知道图象上的点与坐标(,())xfx是一一对应的2.掌握作函数图象的常用方法3.能用函数的图象求解值域,比较大小等问题教学重点与难点1.函数图象的作法2.对函数图象的理解,函数图象的应用教法与学法:自主学习,合作探究一.问题情境:1.初中我们已研究过一次函数,二次函数及反比例函数,你能否快速作出它们的图象?2.你知道函数的图象是怎么定义的吗?3.你知道作函数图象的常用方法有哪些吗?4.你会用函数的图象求解值域,比较函数值的大小吗?二.自主学习:自学课本第2528页,并思考以上四个问题三.合作探究:探究1:函数图象的概念将自变量的一个值0x作为横坐标,相应的函数值0()fx作为纵坐标,就得到坐标平面上的一个点00(,())xfx,当自变量取遍定义域A中的每一个值时,就得到一系列这样的点,所有这些点组成的集合为{(,())|}xfxxA,即{(,)|(),}xyyfxxA,所有这些点组成的图形就是函数()fx的图象。例1.下列图形中可以作为函数图象的是_____________(1)(2)(3)(4)变式:1.下列图形中可以作为函数图象的是_____________1(1)(2)(3)2.下列图形中可以作为函数图象的是_____________(1)(2)(3)(4)探究2:函数图象的作法1.回顾一些基本初等函数的图象:(1)yxyxykx,,(2)11,,kyyyxxx-(3)2222,,1,4yxyxyxyx(4)0,y=2,y=cy(c为任一常数)2.探求函数图象的作法:2例2.试画出下列函数的图象:(1)()35,(2,4]fxxx2(2)()23,0,3fxxxx5(3)()2fxx(4)()fxx总结:1.特征法:(如一次函数的特征是两点:与x轴和y轴的交点,二次函数的特征是:开口,顶点,与x轴和y轴的交点)2.平移变换法:3.描点法:练习:课本第页练习第1题探究3:函数图象的简单应用:例3.试画出函数2()1fxx的图象,并根据图象回答下列问题:(1)比较(2),(1),(3)fff的大小(2)若120xx,试比较1()fx与2()fx的大小练习:课本28页练习第3题思考题:求函数2(),[1,2]fxxx的值域总结:函数()yfx的图象在x轴上的射影构成的集合对应着函数的定义域,在y轴上的射影构成的集合对应着函数的值域。四.课时小结:(1)函数图象的概念(2)函数图象的作法(3)函数图象的应用五.作业:1.课本第29页第3题2.画出243,[3,3]yxxx图象,并求其值域3