高中数学： 平面向量数量积的坐标表示、模、夹角优质课教案新课标人教A版必修4VIP免费

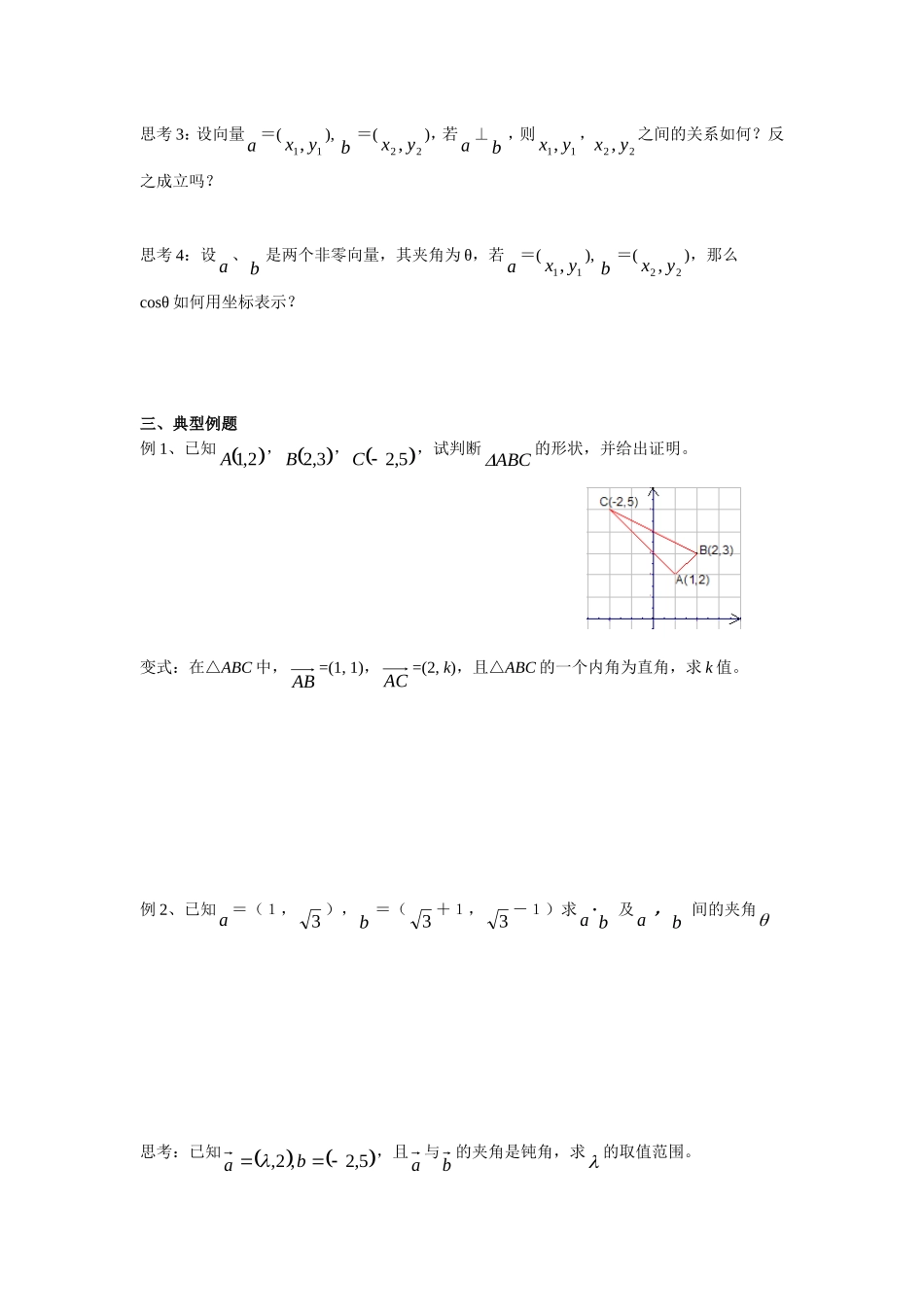
2.4.2平面向量数量积的坐标表示、模、夹角教学目标：1、掌握平面向量数量积的坐标表示方法2、掌握向量垂直的坐标表示的条件，及平面内两点间的距离公式.3、能用平面向量数量积的坐标表示解决有关长度、角度、垂直等几何问题.4、培养学生数形结合、转化与化归的数学思想教学重点：平面向量数量积的坐标表示教学难点：平面向量数量积的坐标表示的综合运用教学过程：一、复习旧知：1．平面向量数量积（内积）的定义：2．已知|a|=6,|b|=4,若a与b的夹角为30°,则a·b=，a2=3．已知向量a、b的夹角为3，|a|=2,|b|=1,则|a+b|=,|a－b|=4．已知|a|=12,|b|=9,a·b=254，则a与b的夹角=二、新课讲解探究（一）：平面向量数量积的坐标表示思考1：设i、j是分别与x轴、y轴同向的两个单位向量，若两个非零向量a＝(11,yx),b＝(22,yx)，则向量a与b用i、j分别如何表示？思考2：对于上述向量i、j，则i2=，j2=，i·j=根据数量积的运算性质，a·b=请用文字描述平面向量数量积的坐标表示探究（二）：向量的模和夹角的坐标表示思考1：设向量a＝(yx,)，利用数量积的坐标表示，︱a︱=思考2：如果表示向量a的有向线段的起点和终点的坐标分别为(11,yx),(22,yx)，那么向量a的坐标如何表示？︱a︱=思考3：设向量a＝(11,yx),b＝(22,yx)，若a⊥b，则11,yx，22,yx之间的关系如何？反之成立吗？思考4：设a、b是两个非零向量，其夹角为θ，若a＝(11,yx),b＝(22,yx)，那么cosθ如何用坐标表示？三、典型例题例1、已知2,1A，3,2B，5,2C，试判断ABC的形状，并给出证明。变式：在△ABC中，AB=(1,1)，AC=(2,k)，且△ABC的一个内角为直角，求k值。例2、已知a＝（１，3），b＝（3＋１，3－１）求a·b及a，b间的夹角思考：已知a5,2,2,b，且a与b的夹角是钝角，求的取值范围。例3、已知b＝(1，1)，a·b＝3，|a－b|＝2，求|a|.四、巩固练习1、若a=(－3，4)，b=(5，2)，则a·b＝（）A.23B.7C.－23D.－72、若a=(－3，4)，b=(5，12)，则a与b夹角的余弦值为（）A.6563B.6533C.6533D.65633、已知|a|=3,b=(1,2)且a∥b,则a的坐标为.4、已知平面向量a＝(1，－3),b＝(4，－2)，若a+b与a垂直，=五、学习小结1、a∥b01221yxyx；a与b共线，使用数乘运算a⊥b02121yyxx；a与b垂直，使用数量积运算，二者有着本质区别.2、若非零向量a与b的夹角为锐角（钝角），则a·b＞0（＜0），反之不成立.3、向量的坐标运算沟通了向量与解析几何的内在联系，解析几何中与角度、距离、平行、垂直有关的问题，可以考虑用向量方法来解决.六、课后作业：P119习题A组：10，12.七、知识拓展平面向量数量积的坐标表示的实质是用代数的观点研究向量（几何）问题，从知识上讲，离不开函数、方程、不等式，特别是二次函数、二元一次、二元二次方程组；从方法上讲，能够体现配方法、解方程组、解方程等数学上的基本的解题方法；从数学思想方面讲，也离不开转化的思想，函数与方程的思想和数形结合的思想向量是代数、三角和几何的载体，是各种思想方法的纽带，具有重要地位。