高中数学空间向量的数乘运算教案人教新课标必修2VIP免费

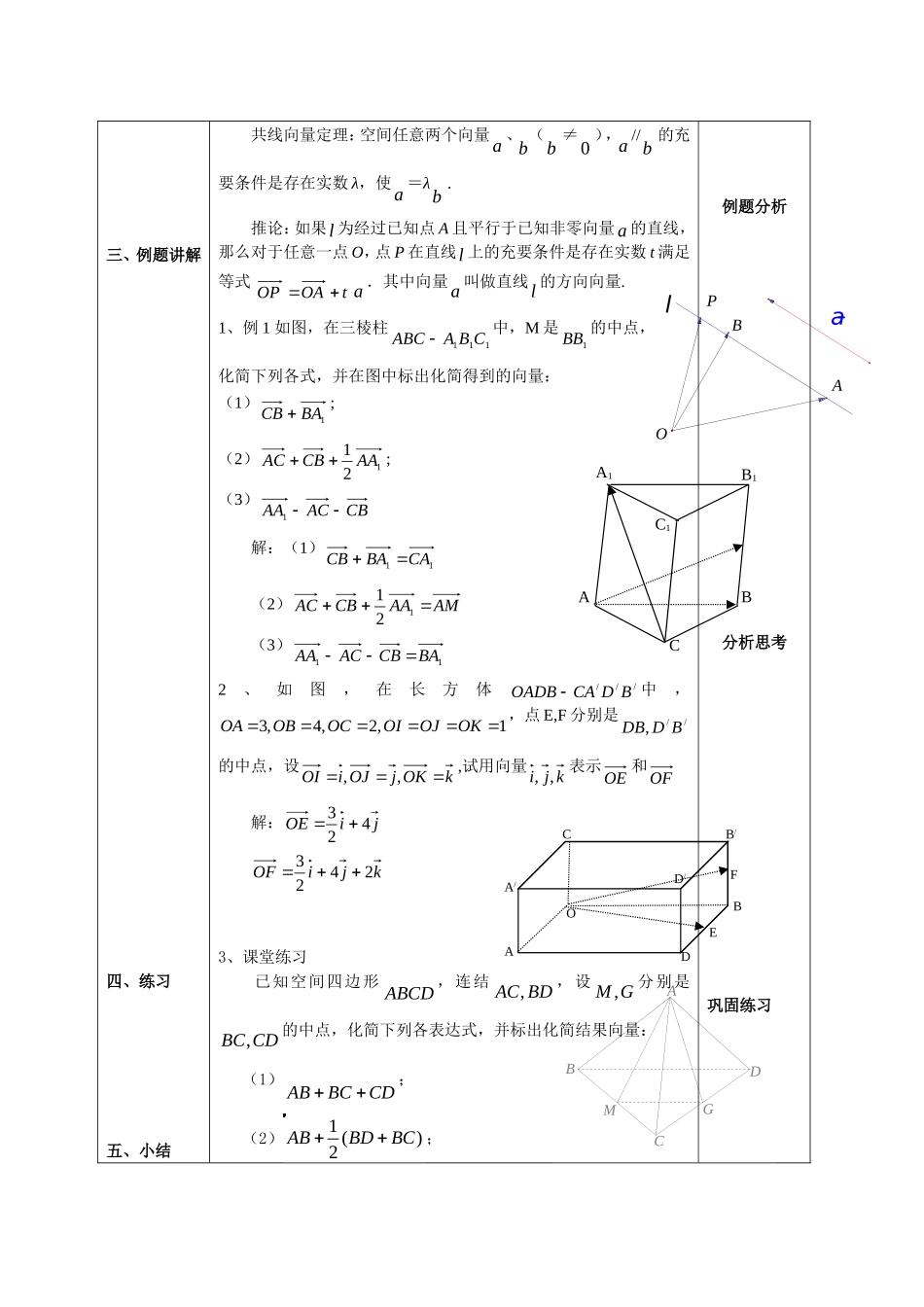
aC'B'A'D'DABC课题：3.1.2空间向量的数乘运算第一课时教学目标：知识与技能：运用类比方法，经历向量及其运算由平面向空间推广的过程；了解空间向量的概念，掌握空间向量的数乘运算及其性质；过程与方法：分组合作，示范交流，应用小结。情感态度与价值观：通过空间向量学习，体会构造的数学思想方法；教学环节教师活动学生活动一、复习引入二、新课导入1．空间向量的概念：在空间，我们把具有大小和方向的量叫做向量奎屯王新敞新疆注：⑴空间的一个平移就是一个向量奎屯王新敞新疆⑵向量一般用有向线段表示奎屯王新敞新疆同向等长的有向线段表示同一或相等的向量奎屯王新敞新疆⑶空间的两个向量可用同一平面内的两条有向线段来表示奎屯王新敞新疆2．空间向量的运算定义：与平面向量运算一样，空间向量的加法、减法与数乘向量运算如下（如图）baABOAOBbaOBOABA)(RaOP运算律：⑴加法交换律：abba⑵加法结合律：)()(cbacba⑶数乘分配律：baba)(3．平行六面体：平行四边形ABCD平移向量a到DCBA的轨迹所形成的几何体，叫做平行六面体，并记作：ABCD－DCBA，它的六个面都是平行四边形，每个面的边叫做平行六面体的棱。4．共线向量与平面向量一样，如果表示空间向量的有向线段所在的直线互相平行或重合，则这些向量叫做共线向量或平行向量．a平行于b记作ba//．当我们说向量a、b共线（或a//b）时，表示a、b的有向线段所在的直线可能是同一直线，也可能是平行直线．5．共线向量定理及其推论：思考思考CBAObbbaaaaBAOlPABCA1B1C1OA/CFED/B/ADB三、例题讲解四、练习五、小结共线向量定理：空间任意两个向量a、b（b≠0），a//b的充要条件是存在实数λ，使a＝λb.推论：如果l为经过已知点A且平行于已知非零向量a的直线，那么对于任意一点O，点P在直线l上的充要条件是存在实数t满足等式tOAOPa．其中向量a叫做直线l的方向向量.1、例1如图，在三棱柱111CBAABC中，M是1BB的中点，化简下列各式，并在图中标出化简得到的向量：（1）1BACB;（2）121AACBAC;（3）CBACAA1解：（1）11CABACB（2）AMAACBAC121（3）11BACBACAA2、如图，在长方体///BDCAOADB中，1,2,4,3OKOJOIOCOBOA，点E,F分别是//,BDDB的中点，设kOKjOJiOI,,,试用向量kji,,表示OE和OF解：jiOE423kjiOF24233、课堂练习已知空间四边形ABCD，连结,ACBD，设,MG分别是,BCCD的中点，化简下列各表达式，并标出化简结果向量：（1）ABBCCD�；（2）1()2ABBDBC�；例题分析分析思考巩固练习BCDMGA课后反思（3）1()2AGABAC�．知识小结：空间向量的定义与运算法则学生掌握本节课内容，课堂气氛活跃