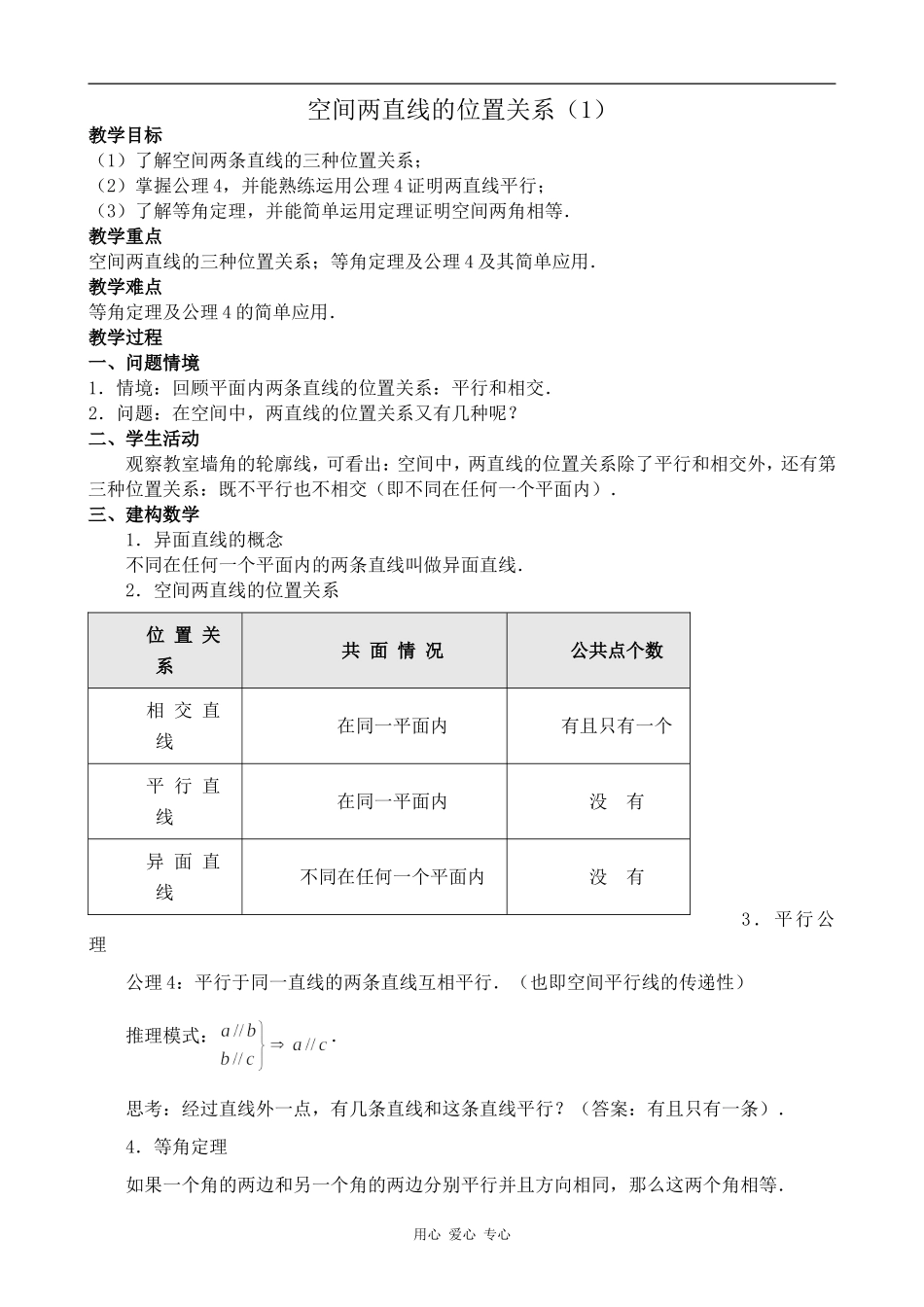
空间两直线的位置关系(1)教学目标(1)了解空间两条直线的三种位置关系;(2)掌握公理4,并能熟练运用公理4证明两直线平行;(3)了解等角定理,并能简单运用定理证明空间两角相等.教学重点空间两直线的三种位置关系;等角定理及公理4及其简单应用.教学难点等角定理及公理4的简单应用.教学过程一、问题情境1.情境:回顾平面内两条直线的位置关系:平行和相交.2.问题:在空间中,两直线的位置关系又有几种呢?二、学生活动观察教室墙角的轮廓线,可看出:空间中,两直线的位置关系除了平行和相交外,还有第三种位置关系:既不平行也不相交(即不同在任何一个平面内).三、建构数学1.异面直线的概念不同在任何一个平面内的两条直线叫做异面直线.2.空间两直线的位置关系3.平行公理公理4:平行于同一直线的两条直线互相平行.(也即空间平行线的传递性)推理模式:.思考:经过直线外一点,有几条直线和这条直线平行?(答案:有且只有一条).4.等角定理如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等.用心爱心专心位置关系共面情况公共点个数相交直线在同一平面内有且只有一个平行直线在同一平面内没有异面直线不同在任何一个平面内没有已知:和的边,并且方向相同,求证:.证明:在和的两边分别截取,∵,∴是平行四边形,∴,同理,∴,即是平行四边形,∴,∴,所以,.思考:如果一个角的两边与另一个角的两边分别平行,那么这两个角的关系如何呢?四、数学运用1.例题:例1.如图,在长方体中,已知分别是的中点,求证:.证明:连结,在中,分别是的中点,∴,又∵,∴,∴四边形是平行四边形,∴,所以,.例2.已知分别是空间四边形四条边的中点,求证:四边形是平行四边形.证明:连结,∵是的边上的中点,∴,同理,,∴,同理,,所以,四边形是平行四边形.思考:立几中“两组对边分别平行”,“一组对边平行且相等”,“两组对边都相等”的四边形是否为平行四边形?为什么?用心爱心专心E1A1B1C1DABCDFABCDGFEHADBBCEDEAC例3.如图,已知是正方体的棱的中点,求证:.分析:设法证明即可.证明:连结,∵分别是棱的中点,∴,∴四边形是平行四边形,∴.又∵,∴,故四边形是平行四边形.∴,同理,又∵、两边的方向相同,所以,.五、回顾小结:1.空间两直线的三种位置关系:平行、相交、异面;2.公理3及等角定理的简单应用.六、课外作业:1.已知正方体中,分别为的中点,试判断下列直线是否平行?2.在正方体中,分别为棱的中点,试证明:.用心爱心专心1A1CABC1DD1BE1A1CABC1DD1B1E用心爱心专心