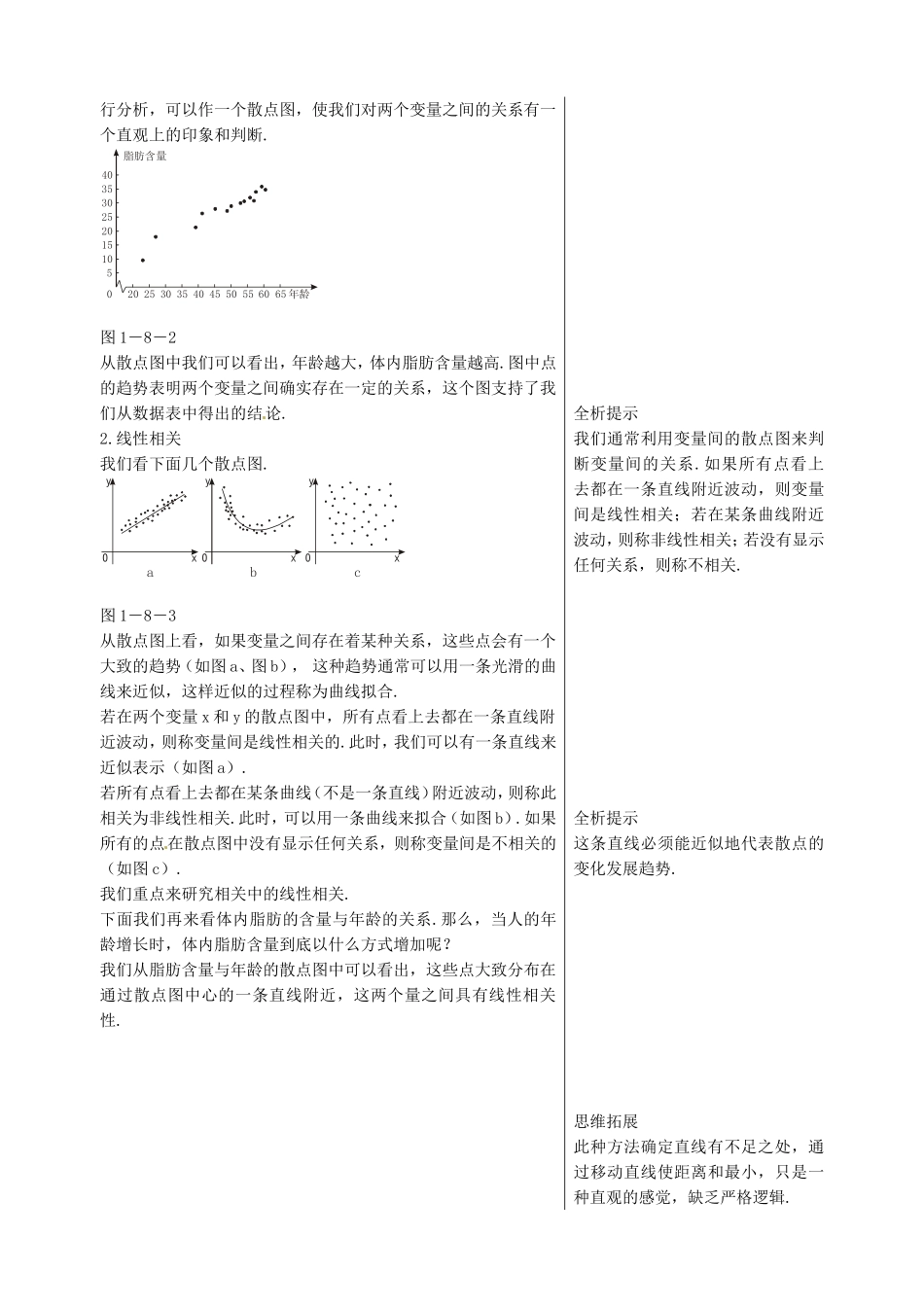
相关性-课文知识点解析全析提示1.散点图为了了解人的身高与体重的关系,我们随机地抽取9名15岁的男生,测得身高、体重如下表:编号123456789身高/cm165157155175168157178160163体重/kg524445555447625053从表中不难看出,同一身高157cm对应着不同的体重44kg和47kg,体重不是身高的函数.如果把身高看作横坐标、体重看作纵坐标,在坐标系中画出对应的点,就会发现,随着身高的增长,体重基本上是呈直线增加的趋势.体重/kg6560555045400150155160165170175180身高/cm图1-8-1在考虑两个量的关系时,为了对变量之间的关系有一个大致的了解,人们通常将变量所对应的点描出来,这些点就组成了变量之间的一个图,通常把这种图叫做变量之间的散点图.散点图的制作通常有两种方法:一是手工绘图;二是用计算机作图.手工作图比较烦琐,也易出现误差,不够精确,我们通常利用计算机作图,简单而准确.下面,我们再看一个例子:在一次对人体脂肪含量和年龄关系的研究中,研究人员得到了一组数据(如下表):人体的脂肪百分比和年龄年龄23273941454950脂肪9.517.821.225.927.526.328.2年龄53545657586061脂肪29.630.231.430.833.535.234.6根据上述数据,人体的脂肪含量与年龄之间存在怎样的关系?一般地,对于某个人来说,他的体内脂肪不一定随年龄增长而增加或减少.但是把很多个体放在一起,这时就可能表现出一定的规律性来.观察表中数据,大体上来看,随着年龄的增长,人体中的脂肪百分比也在增加.为了确定这一细节,我们需要对数据进为了使取得的样本具有广泛代表性,应采用抽样的方法,如简单随机抽样、分层抽样等抽样方法.思维拓展如果身高和体重存在函数关系,则图象应为平滑的直线或曲线,或为均匀分散在直线或曲线上的点.全析提示可利用计算机中的电子表格软件制作两个变量间的散点图.全析提示要从实践中不断提高分析数据的能力,我们往往借助于列表和作图来分析数据.全析提示在作散点图时,假设年龄影响体内脂肪含量,按习惯,以x轴表示年龄,以y轴表示脂肪含量.行分析,可以作一个散点图,使我们对两个变量之间的关系有一个直观上的印象和判断.脂肪含量40353025201510520253035404550556065年龄0图1-8-2从散点图中我们可以看出,年龄越大,体内脂肪含量越高.图中点的趋势表明两个变量之间确实存在一定的关系,这个图支持了我们从数据表中得出的结论.2.线性相关我们看下面几个散点图.xyOaxyObxyOc图1-8-3从散点图上看,如果变量之间存在着某种关系,这些点会有一个大致的趋势(如图a、图b),这种趋势通常可以用一条光滑的曲线来近似,这样近似的过程称为曲线拟合.若在两个变量x和y的散点图中,所有点看上去都在一条直线附近波动,则称变量间是线性相关的.此时,我们可以有一条直线来近似表示(如图a).若所有点看上去都在某条曲线(不是一条直线)附近波动,则称此相关为非线性相关.此时,可以用一条曲线来拟合(如图b).如果所有的点在散点图中没有显示任何关系,则称变量间是不相关的(如图c).我们重点来研究相关中的线性相关.下面我们再来看体内脂肪的含量与年龄的关系.那么,当人的年龄增长时,体内脂肪含量到底以什么方式增加呢?我们从脂肪含量与年龄的散点图中可以看出,这些点大致分布在通过散点图中心的一条直线附近,这两个量之间具有线性相关性.全析提示我们通常利用变量间的散点图来判断变量间的关系.如果所有点看上去都在一条直线附近波动,则变量间是线性相关;若在某条曲线附近波动,则称非线性相关;若没有显示任何关系,则称不相关.全析提示这条直线必须能近似地代表散点的变化发展趋势.思维拓展此种方法确定直线有不足之处,通过移动直线使距离和最小,只是一种直观的感觉,缺乏严格逻辑.脂肪含量40353025201510520253035404550556065年龄0图1-8-4那么,如何确定这条直线呢?这条直线有什么特点呢?要想确定这条直线,必须先弄清该直线的特点.这条直线代表了所有散点的发展变化趋势,也就是说所有散点到该直线的距离最小,使散点都尽可能地处在该直线的附近.下面我们看几种确定这条直线的方法.(1)我们可以采用测量的方法,先画出一条直线,测量出各点与它...