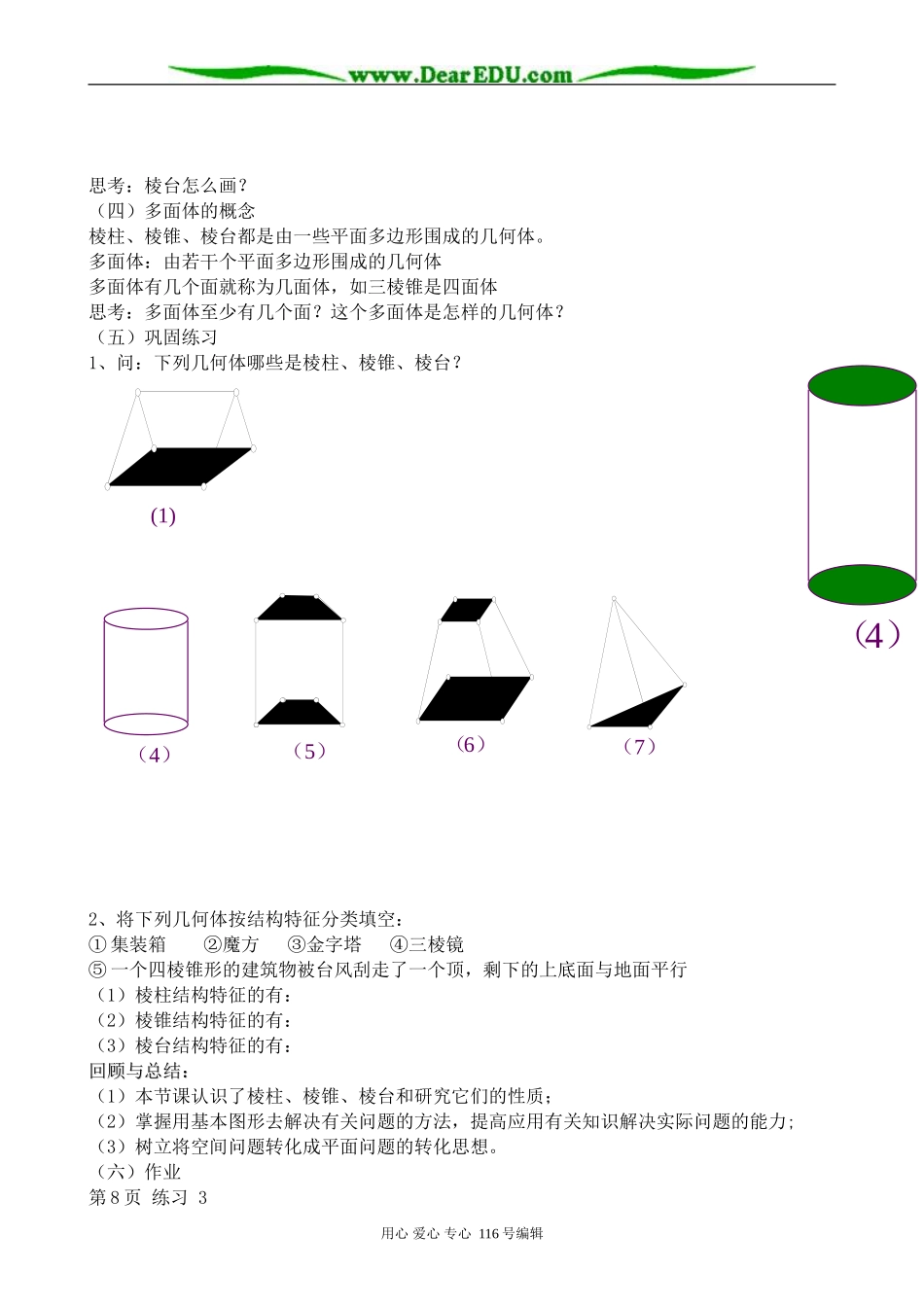
棱柱、棱锥和棱台(1)教学目标:1、了解多面体、棱柱、棱锥、棱台的定义、性质及它们之间的关系;2、掌握棱柱、棱台的画法;3、结合模型、动态的或静态的直观图,了解、认识和研究各种几何体;4、培养空间(三维空间)与平面(二维空间)问题相互转化(升降维)的思想方法。教学重点:棱柱、棱锥、棱台的定义、性质及它们之间的关系。教学难点:空间(三维空间)与平面(二维空间)问题相互转化(升降维)。教学过程:(一)棱柱的概念1、思考:我们常见的一些物体,例如三棱镜,方砖以及螺杆的头部等,它们有什么共同的特点:平移:指将一个图形上所有点按某一确定的方向移动相同的距离2.定义:一般地,由一个平面多边形沿某一方向平移形成的空间几何体叫做棱柱。思考:上图的棱柱分别是由何种多边形平移得到?3.棱柱的元素:a.平移起止位置的两个面叫做棱柱的底面。b.多边形的边平移所形成的面叫做棱柱的侧面。c.两个侧面的公共边叫做棱柱的侧棱。d.侧面与底的公共顶点叫做棱柱的顶点。4.棱柱的分类:按底面的边数分为:棱柱的底面可以是三角形、四边形、五边形、……把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱、……5.棱柱的表示法:用平行的两底面多边形的字母表示棱柱,如:棱柱ABCDE-A1B1C1D1E16.棱柱的性质:a.侧棱都相等,侧面是平行四边形;b.两个底面是全等的多边形,且对应边互相平行;c.过不相邻的两条侧棱的截面是平行四边形(二)棱锥的概念思考:看下面两个图形有何变化?用心爱心专心116号编辑棱锥的定义:当棱柱的一个底面收缩为一个点时,得到的几何体叫棱锥。与棱柱相仿,棱锥中常用名称的含义侧面:有公共顶点的各三角形面底面(底):余下的那个多边形侧棱:两个相邻侧面的公共边顶点:各侧面的公共点思考:有一个面是多边形其余各面是三角形,这个多面体是棱锥吗?(三)棱台的概念思考:用一个平行于棱锥底面的平面去截棱锥,得到两个怎么样的几何体?棱台是棱锥被平行于底面的一个平面所截后,截面和底面之间的部分棱台的性质:上下底面平行,且对应边成比例。只有这样,才保证各侧棱交于一点。提问:如图的几何体是不是棱台?为什么?例1:画一个六棱柱和一个五棱锥。六棱柱的画法棱锥的的画法用心爱心专心116号编辑ABCDES思考:棱台怎么画?(四)多面体的概念棱柱、棱锥、棱台都是由一些平面多边形围成的几何体。多面体:由若干个平面多边形围成的几何体多面体有几个面就称为几面体,如三棱锥是四面体思考:多面体至少有几个面?这个多面体是怎样的几何体?(五)巩固练习1、问:下列几何体哪些是棱柱、棱锥、棱台?2、将下列几何体按结构特征分类填空:①集装箱②魔方③金字塔④三棱镜⑤一个四棱锥形的建筑物被台风刮走了一个顶,剩下的上底面与地面平行(1)棱柱结构特征的有:(2)棱锥结构特征的有:(3)棱台结构特征的有:回顾与总结:回顾与总结:(1)本节课认识了棱柱、棱锥、棱台和研究它们的性质;(2)掌握用基本图形去解决有关问题的方法,提高应用有关知识解决实际问题的能力;(3)树立将空间问题转化成平面问题的转化思想。(六)作业第8页练习3用心爱心专心116号编辑(1)(4)(6)(7)(4)(5)用心爱心专心116号编辑