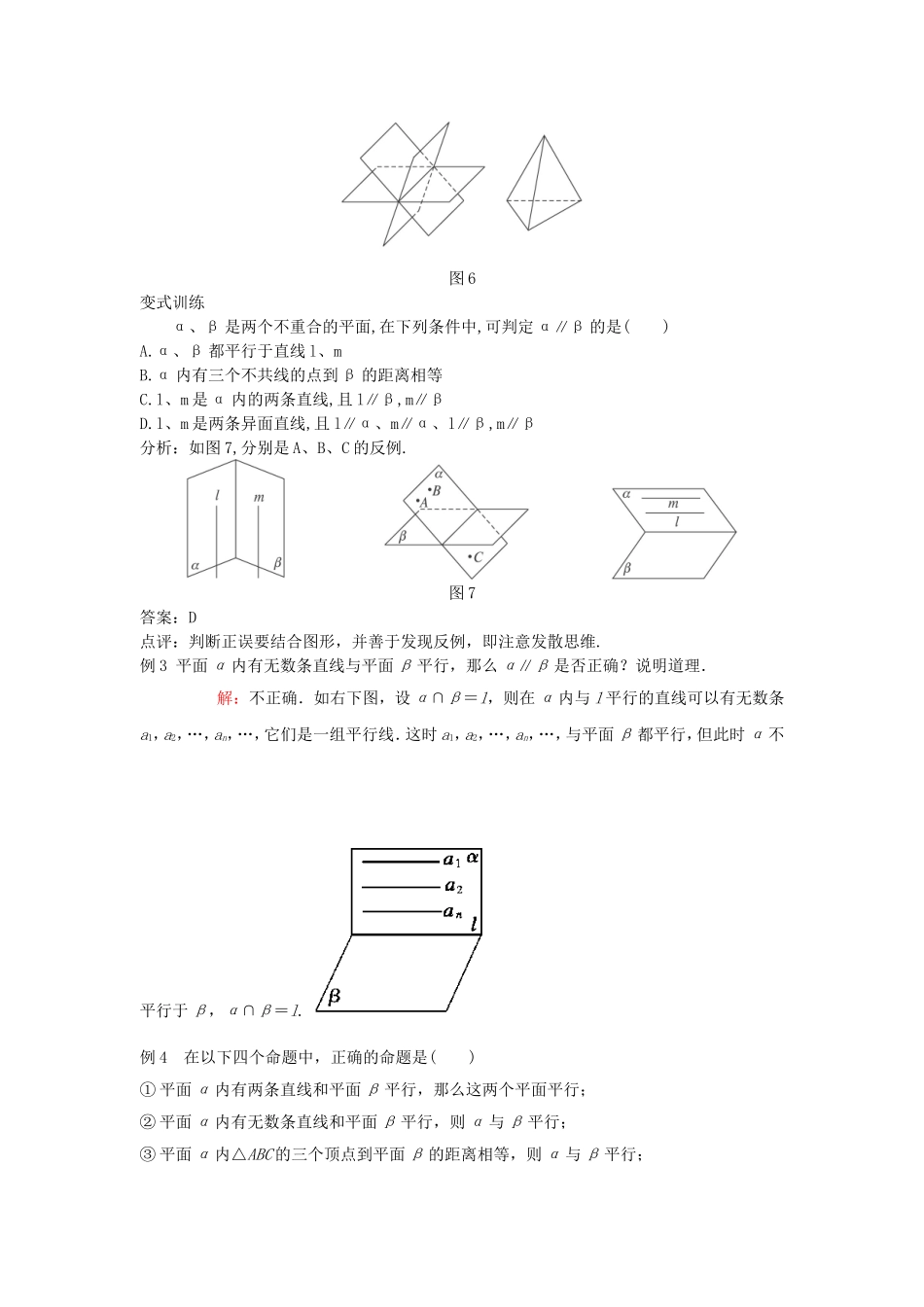
平面与平面之间的位置关系【本节教材分析】(一)三维目标1.知识与技能结合图形正确理解空间中平面与平面之间的位置关系2.过程与方法进一步熟悉文字语言、图形语言、符号语言的相互转换.3.情感态度与价值观进一步培养学生的空间想象能力,培养学生全面思考问题的能力.(二)教学重点空间平面与平面之间的位置关系。平面与平面的相交和平行.(三)教学难点用图形表达直线与平面、平面与平面的位置关系。(四)教学建议空间中平面与平面之间的位置关系是立体几何中最重要的位置关系,平面与平面的相交和平行是本节的重点和难点.空间中平面与平面之间的位置关系是根据交点个数来定义的,要求学生在公理3的基础上会判断平面与平面之间的位置关系.本节重点是结合图形判断空间中平面与平面之间的位置关系.【新课导入设计】导入一:(情境导入)拿出两本书,看作两个平面,上下、左右移动和翻转,它们之间的位置关系有几种?导入二:(事例导入)观察长方体(图1),围成长方体ABCD—A′B′C′D′的六个面,两两之间的位置关系有几种?图1【课堂结构】提出问题①什么叫做两个平面平行?②两个平面平行的画法.③回忆两个平面相交的依据.④什么叫做两个平面相交?⑤用三种语言描述平面与平面之间的位置关系.活动:先让学生思考,后再回答,经教师提示、点拨,对回答正确的学生及时表扬,对回答不准确的学生提示引导考虑问题的思路.问题①引导学生回忆直线与平面平行的定义.问题②怎样体现两个平面平行的特点.问题③两个平面有一个公共点,两平面是否相交.问题④回忆公理三.问题⑤鼓励学生自我训练.讨论结果:①两个平面平行——没有公共点.②画两个互相平行的平面时,要注意使表示平面的平行四边形的对应边平行,如图2.图2图3③如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线.此时,就说两平面相交,交线就是公共点的集合,这就是公理3.如图3,用符号语言表示为:P∈α且P∈βα∩β=l,且P∈l.④两个平面相交——有一条公共直线.⑤如果两个平面没有公共点,则两平面平行若α∩β=,则α∥β.如果两个平面有一条公共直线,则两平面相交若α∩β=AB,则α与β相交.两平面平行与相交的图形表示如图4.图4例题讲解例1已知平面α,β,直线a,b,且α∥β,aα,bβ,则直线a与直线b具有怎样的位置关系?活动:学生自己思考或讨论,再写出正确的答案.教师在学生中巡视,发现问题及时纠正,并及时评价.解:如图5,直线a与直线b的位置关系为平行或异面.图5例2如果三个平面两两相交,那么它们的交线有多少条?画出图形表示你的结论.解:三个平面两两相交,它们的交线有一条或三条,如图6.图6变式训练α、β是两个不重合的平面,在下列条件中,可判定α∥β的是()A.α、β都平行于直线l、mB.α内有三个不共线的点到β的距离相等C.l、m是α内的两条直线,且l∥β,m∥βD.l、m是两条异面直线,且l∥α、m∥α、l∥β,m∥β分析:如图7,分别是A、B、C的反例.图7答案:D点评:判断正误要结合图形,并善于发现反例,即注意发散思维.例3平面α内有无数条直线与平面β平行,那么α∥β是否正确?说明道理.解:不正确.如右下图,设α∩β=l,则在α内与l平行的直线可以有无数条a1,a2,…,an,…,它们是一组平行线.这时a1,a2,…,an,…,与平面β都平行,但此时α不平行于β,α∩β=l.例4在以下四个命题中,正确的命题是()①平面α内有两条直线和平面β平行,那么这两个平面平行;②平面α内有无数条直线和平面β平行,则α与β平行;③平面α内△ABC的三个顶点到平面β的距离相等,则α与β平行;A.③B.②C.②③D.都不正确解析:如图所示正方体ABCD-A1B1C1D1中,对于①,平面A1D1DA中,AD∥平面A1B1C1D1,分别取AA1、DD1的中点E,F,连结EF,则知EF∥平面A1B1C1D1.但平面AA1D1D与平面A1B1C1D1是相交的,交线为A1D1,故命题①错.对于②,在正方体ABCD-A1B1C1D1中的面AA1D1D中,与AD平行的直线有无数条,但平面AA1D1D与平面A1B1C1D1不平行而是相交于直线A1D1,故②是错的.对于③,在正方体ABCD-A1B1C1D1中,取AA1,DD1,BB1,CC1中点E,F,G,H,A1,B,C到平面EFHG的距离相...