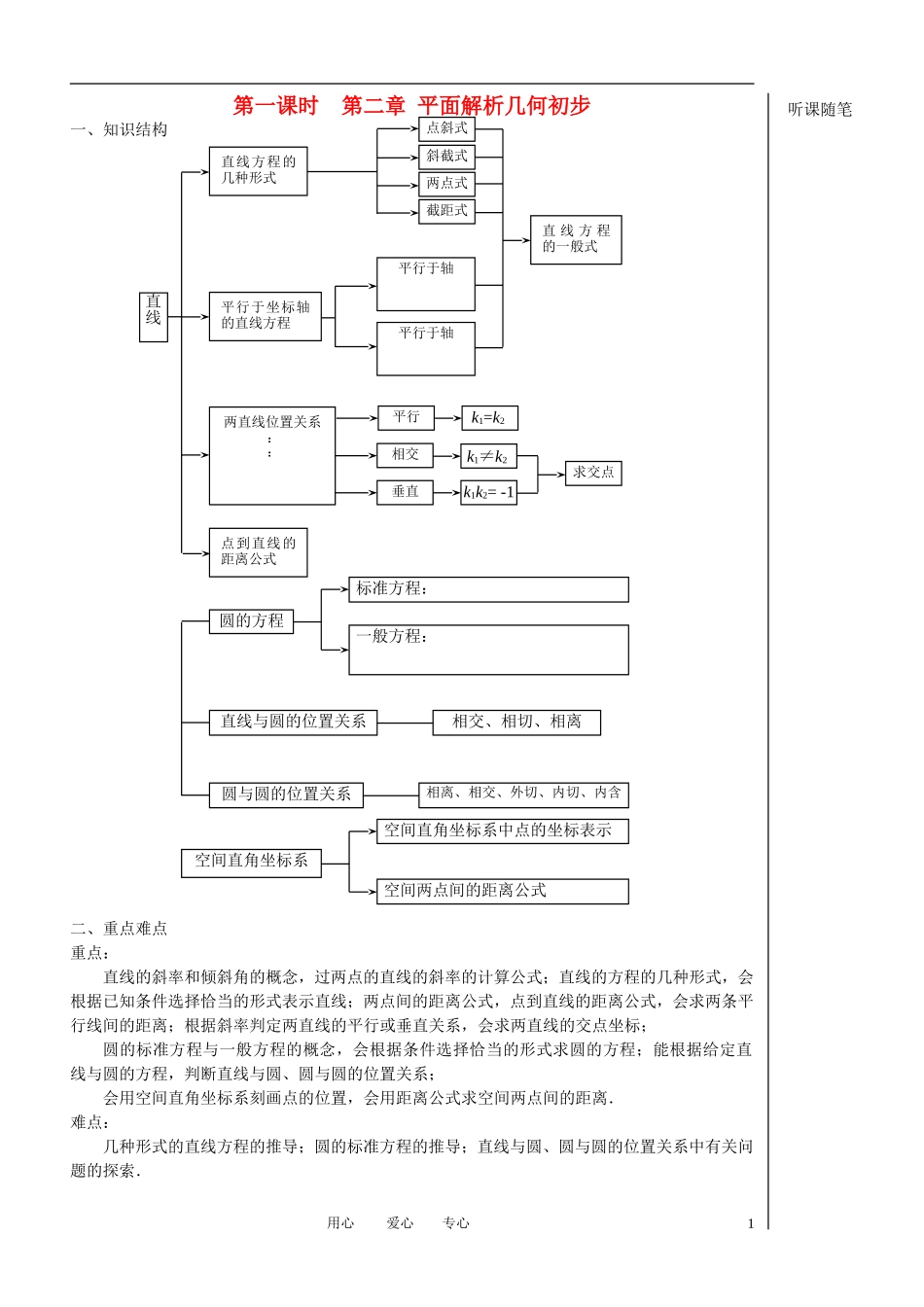
第一课时第二章平面解析几何初步一、知识结构二、重点难点重点:直线的斜率和倾斜角的概念,过两点的直线的斜率的计算公式;直线的方程的几种形式,会根据已知条件选择恰当的形式表示直线;两点间的距离公式,点到直线的距离公式,会求两条平行线间的距离;根据斜率判定两直线的平行或垂直关系,会求两直线的交点坐标;圆的标准方程与一般方程的概念,会根据条件选择恰当的形式求圆的方程;能根据给定直线与圆的方程,判断直线与圆、圆与圆的位置关系;会用空间直角坐标系刻画点的位置,会用距离公式求空间两点间的距离.难点:几种形式的直线方程的推导;圆的标准方程的推导;直线与圆、圆与圆的位置关系中有关问题的探索.用心爱心专心1听课随笔直线直线方程的一般式两直线位置关系::平行于坐标轴的直线方程平行于轴平行于轴直线方程的几种形式点斜式斜截式两点式截距式垂直k1k2=-1平行k1=k2相交k1≠k2求交点点到直线的距离公式圆的方程标准方程:一般方程:直线与圆的位置关系圆与圆的位置关系相交、相切、相离相离、相交、外切、内切、内含空间直角坐标系空间直角坐标系中点的坐标表示空间两点间的距离公式第1课直线的斜率(1)【学习导航】知识网络学习要求1.理解直线的斜率的概念;2.掌握过两点的直线斜率的计算公式.自学评价1.直线的斜率:已知两点1122(,),(,)PxyQxy,如果x1x2那么,直线PQ的斜率为k;此时,斜率也可看成是.【精典范例】例1:如图,直线123,,lll都经过点(3,2)P,又123,,lll分别经过点12(2,1),(4,2)QQ,3(3,2)Q,试计算直线123,,lll的斜率.【解】例2:已知直线l经过点(,2)Am、2(1,2)Bm,求直线l的斜率.【解】例3:经过点(3,2)画直线,使直线的斜率分别为:(1)34;(2)45.【解】【选修延伸】一、直线斜率与三点共线例4:已知三点(,2),(3,7),(2,9)AaBCa在一条直线上,求实数a的值.【解】思维点拔:任何直线都有倾斜角和斜率吗?根据直线倾斜角和斜率的概念,任何直线都有倾斜角.特别地,当直线与x轴平行或重合时,倾斜角为0;当直线与x轴垂直时,倾斜角为90,此时直线斜率不存在.因此,除倾斜角为用心爱心专心直线的斜率计算公式概念听课随笔290的直线外,其他直线都有斜率.追踪训练1.ABC的三个顶点(3,2),(4,1)AB,(0,1)C,写出ABC三边所在直线的斜率:ABk,BCk,ACk.2.求证:(1,5),(0,2),(2,8)ABC三点共线.3.已知过点(1,2)m,(,3)mm的直线l的斜率为3,则实数m的值为.4、设点A(-1,1),B(x,2),C(-2,y)为直线l上三点,已知直线的斜率k=2,则x=.用心爱心专心学生质疑教师释疑听课随笔3