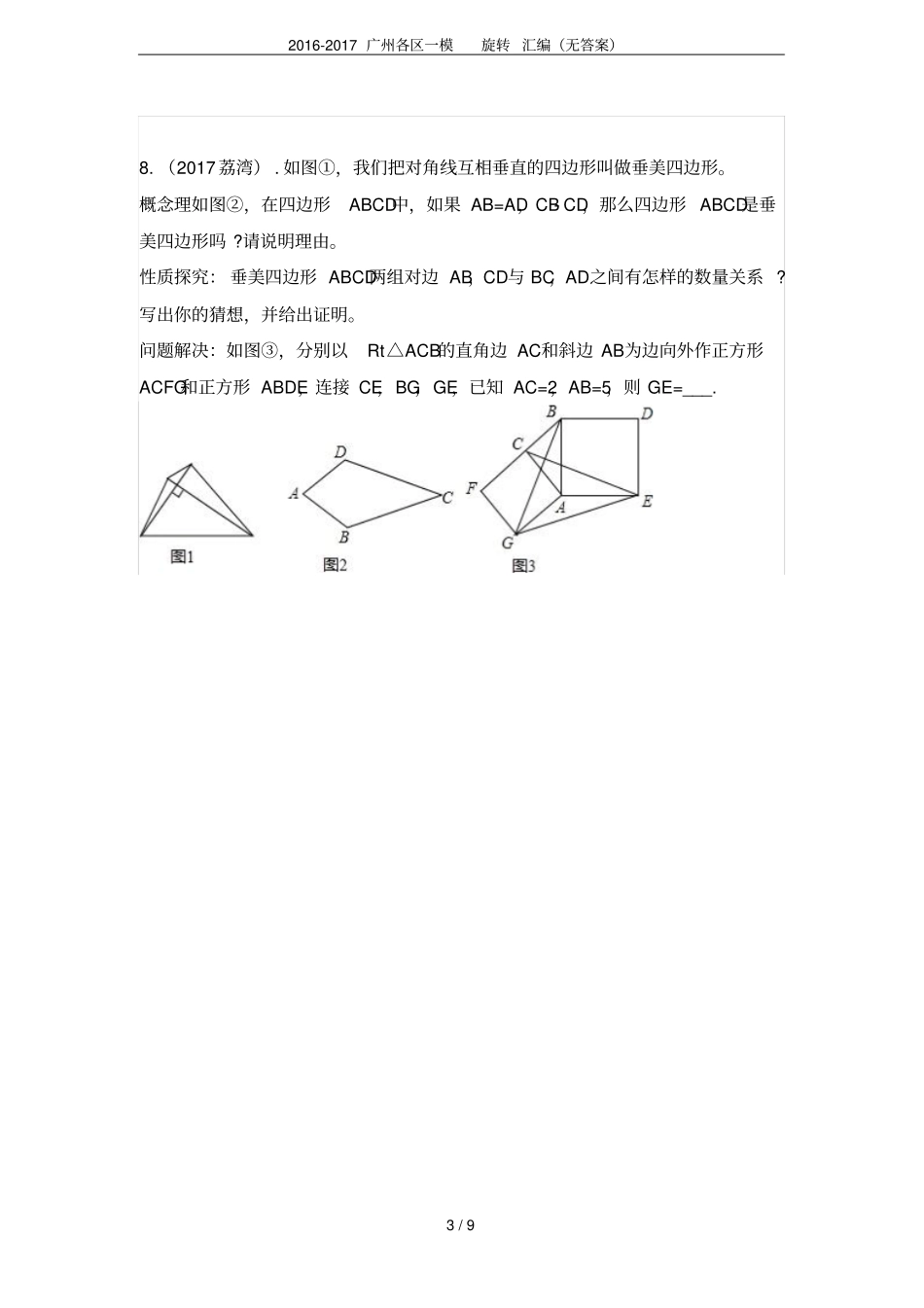
2016-2017广州各区一模旋转汇编(无答案)1/91(2017天河).正方形ABCD中,E为DC边上一点,且DE=1,将AE绕点E顺时针旋转90°得到EF,连接AF,FC,则FC=___.2.(2017番禺)如图,已知在Rt△AOB中,点A(1,2),∠OBA=90°,OB在x轴上,将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y=kx(k>0)上,则k的值为()A.1B.2C.3D.43.(2016番禺)如图,在平面直角坐标系中,矩形OABC的顶点B坐标为(8,4),将矩形OABC绕点O逆时针旋转,使点B落在y轴上的点B′处,得到矩形OA′B′C′,OA′与BC相交于点D,则经过点D的反比例函数解析式是___.2016-2017广州各区一模旋转汇编(无答案)2/94.(2016花都)如图,是正六边形硬纸片ABCDEF在桌面上的起始位置,它的边长为2cm,若它沿直线l不滑行地翻滚一周,则正六边形的中心O运动的路程为___cm.5.(2017增城)如图,在等边△ABC中,AB=10,D是BC的中点,将△ABD绕点A旋转后得到△ACE,则线段DE的长度为___.6.(2017广大附)如图,AC是矩形ABCD的对角线,AB=2,BC=23√,点E,F分别是线段AB,AD上的点,连接CE,CF.当∠BCE=∠ACF,且CE=CF时,AE+AF=___.7.(2016白云)在平面直角坐标系中,Rt△OAB的顶点A的坐标为(3√,1),若将△OAB绕O点,逆时针旋转60°后,B点到达B′点,则点B′的坐标是___.2016-2017广州各区一模旋转汇编(无答案)3/98.(2017荔湾).如图①,我们把对角线互相垂直的四边形叫做垂美四边形。概念理如图②,在四边形ABCD中,如果AB=AD,CB-CD,那么四边形ABCD是垂美四边形吗?请说明理由。性质探究:垂美四边形ABCD两组对边AB,CD与BC,AD之间有怎样的数量关系?写出你的猜想,并给出证明。问题解决:如图③,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=2,AB=5,则GE=___.2016-2017广州各区一模旋转汇编(无答案)4/99.(2016海珠)已知正方形ABCD和正方形CEFG,连结AF交BC于点O,点P是AF的中点,过点P作PH⊥DG于H,CD=2,CG=1.(1)如图1,点D.C.G在同一直线上,点E在BC边上,求PH的长;(2)把正方形CEFG绕着点C逆时针旋转α(0°<α<180°)①如图2,当点E落在AF上时,求CO的长;②如图3,当DG=7√时,求PH的长。2016-2017广州各区一模旋转汇编(无答案)5/910.(2016天河)类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做等邻边四边形。(1)如图1,四边形ABCD中,AC平分∠BAD,∠B=∠D.求证:四边形ABCD为等邻边四边形。(2)如图2,Rt△ABC中,∠ABC=90°,AB=2,BC=1,将△ABC沿∠ABC的平分线BB′的方向平移,得到△A′B′C′,连接AA′、BC′,若平移后的四边形ABC′A′是等邻边四边形,且满足BC′=AB,求平移的距离。(3)如图3,在等邻边四边形ABCD中,AB=AD,∠BAD+∠BCD=90°,AC和BD为四边形对角线,△BCD为等边三角形,试探究AC和AB的数量关系。2016-2017广州各区一模旋转汇编(无答案)6/911.(2017白云)已知,如图,△ABC的三条边BC=a,CA=b,AB=c,D为△ABC内一点,且∠ADB=∠BDC=∠CDA=120°,DA=u,DB=v,DC=w.(1)若∠CBD=18°,则∠BCD=___°;(2)将△ACD绕点A顺时针方向旋转90°到△AC′D′,画出△AC′D′,若∠CAD=20°,求∠CAD′度数;(3)试画出符合下列条件的正三角形:M为正三角形内的一点,M到正三角形三个顶点的距离分别为a、b、c,且正三角形的边长为u+v+w,并给予证明。2016-2017广州各区一模旋转汇编(无答案)7/912.(2017花都)已知⊙O中,弦AB=AC,点P是∠BAC所对弧上一动点,连接PA,PB.(1)如图①,把△ABP绕点A逆时针旋转到△ACQ,连接PC,求证:∠ACP+∠ACQ=180°;(2)如图②,若∠BAC=60°,试探究PA、PB、PC之间的关系。(3)若∠BAC=120°时,(2)中的结论是否成立?若是,请证明;若不是,请直接写出它们之间的数量关系,不需证明。2016-2017广州各区一模旋转汇编(无答案)8/913.(2016南沙)已知,在△ABC中,AB=AC.过A点的直线a从与边AC重合的位置开始绕点A按顺时针方向旋转角θ,直线a交BC边于点P(点P不与点B.点C重合),△BMN的边MN始终在直线a上(点M在点N的上方),且BM=BN,连接CN.(1)当∠BAC=∠MBN=90°时,①如图a,当θ=45°时,∠ANC的度数为___;②如图b,当θ≠45°时,①中的结论...