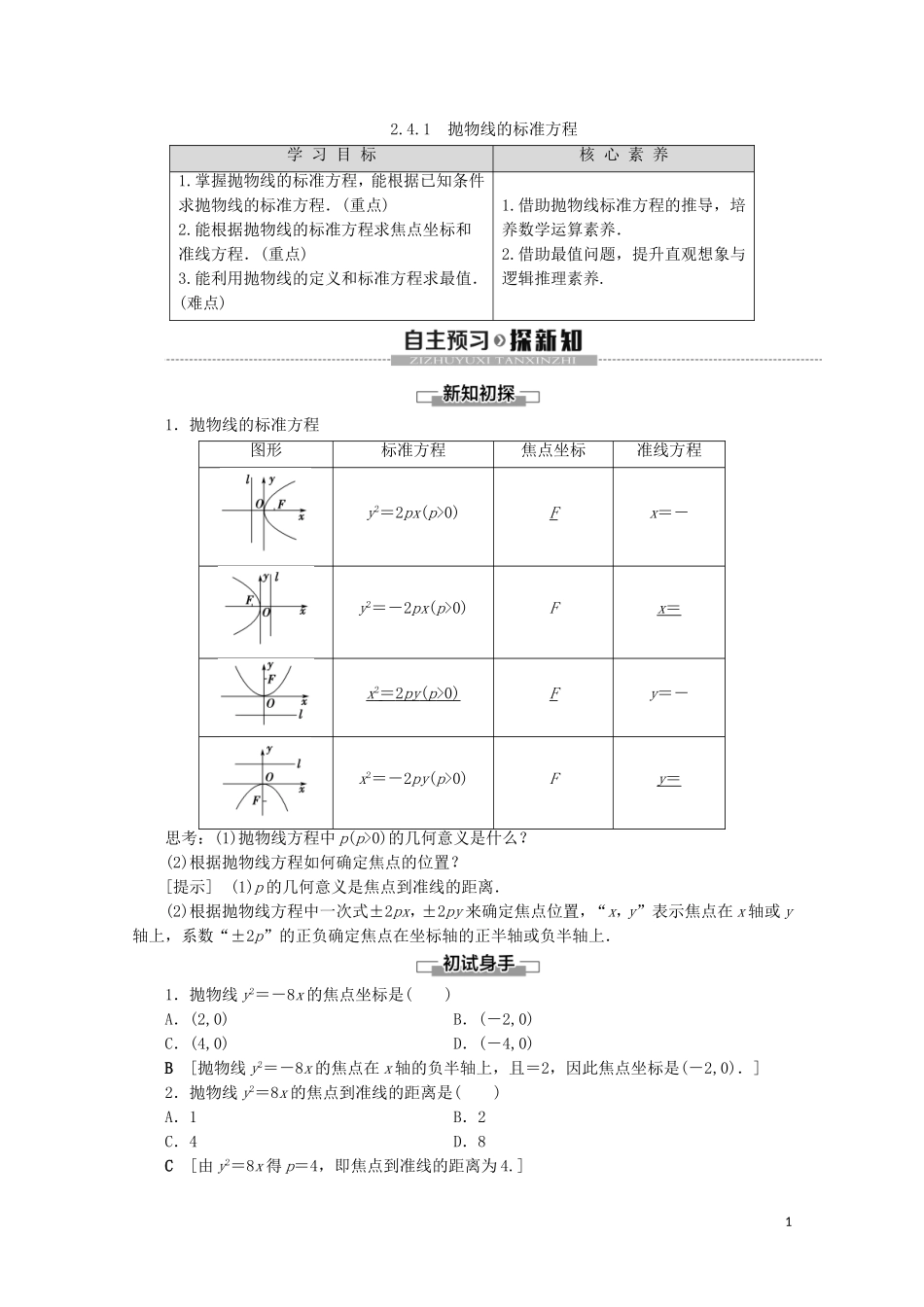
2.4.1抛物线的标准方程学习目标核心素养1.掌握抛物线的标准方程,能根据已知条件求抛物线的标准方程.(重点)2.能根据抛物线的标准方程求焦点坐标和准线方程.(重点)3.能利用抛物线的定义和标准方程求最值.(难点)1.借助抛物线标准方程的推导,培养数学运算素养.2.借助最值问题,提升直观想象与逻辑推理素养.1.抛物线的标准方程图形标准方程焦点坐标准线方程y2=2px(p>0)Fx=-y2=-2px(p>0)Fx=x2=2py(p>0)Fy=-x2=-2py(p>0)Fy=思考:(1)抛物线方程中p(p>0)的几何意义是什么?(2)根据抛物线方程如何确定焦点的位置?[提示](1)p的几何意义是焦点到准线的距离.(2)根据抛物线方程中一次式±2px,±2py来确定焦点位置,“x,y”表示焦点在x轴或y轴上,系数“±2p”的正负确定焦点在坐标轴的正半轴或负半轴上.1.抛物线y2=-8x的焦点坐标是()A.(2,0)B.(-2,0)C.(4,0)D.(-4,0)B[抛物线y2=-8x的焦点在x轴的负半轴上,且=2,因此焦点坐标是(-2,0).]2.抛物线y2=8x的焦点到准线的距离是()A.1B.2C.4D.8C[由y2=8x得p=4,即焦点到准线的距离为4.]13.抛物线x=4y2的准线方程是()A.y=B.y=-1C.x=-D.x=C[由x=4y2得y2=x,故准线方程为x=-.]4.已知抛物线的焦点坐标是(0,-3),则抛物线的标准方程是________.x2=-12y[ =3,∴p=6,∴x2=-12y.]求抛物线的焦点及准线【例1】(1)抛物线2y2-3x=0的焦点坐标是________,准线方程是________.(2)若抛物线的方程为y=ax2(a≠0),则抛物线的焦点坐标为________,准线方程为________.(1)x=-(2)y=-[(1)抛物线2y2-3x=0的标准方程是y2=x,∴2p=,p=,=,焦点坐标是,准线方程是x=-.(2)抛物线方程y=ax2(a≠0)化为标准形式:x2=y,当a>0时,则2p=,解得p=,=,∴焦点坐标是,准线方程是y=-.当a<0时,则2p=-,=-.∴焦点坐标是,准线方程是y=-,综上,焦点坐标是,准线方程是y=-.]求抛物线的焦点及准线步骤1.把解析式化为抛物线标准方程形式.2.明确抛物线开口方向.3.求出抛物线标准方程中p的值.4.写出抛物线的焦点坐标或准线方程.1.求抛物线y=-mx2(m>0)的焦点坐标和准线方程.[解]抛物线y=-mx2(m>0)的标准方程是x2=-y. m>0,∴2p=,=,焦点坐标是,准线方程是y=.求抛物线的标准方程【例2】根据下列条件确定抛物线的标准方程.(1)关于y轴对称且过点(-1,-3);(2)过点(4,-8);(3)焦点在x-2y-4=0上.[思路探究](1)用待定系数法求解;(2)因焦点位置不确定,需分类讨论求解;(3)焦点是直线x-2y-4=0与坐标轴的交点,应先求交点再写方程.[解](1)法一:设所求抛物线方程为x2=-2py(p>0),将点(-1,-3)的坐标代入方程,得(-1)2=-2p·(-3),解得p=,所以所求抛物线方程为x2=-y.法二:由已知,抛物线的焦点在y轴上,因此设抛物线的方程为x2=my(m≠0).又抛物线过2点,所以1=m·(-3),即m=-,所以所求抛物线方程为x2=-y.(2)法一:设所求抛物线方程为y2=2px(p>0)或x2=-2p′y(p′>0),将点(4,-8)的坐标代入y2=2px,得p=8;将点(4,-8)的坐标代入x2=-2p′y,得p′=1.所以所求抛物线方程为y2=16x或x2=-2y.法二:当焦点在x轴上时,设抛物线的方程为y2=nx(n≠0),又抛物线过点(4,-8),所以64=4·n,即n=16,抛物线的方程为y2=16x;当焦点在y轴上时,设抛物线的方程为x2=my(m≠0),又抛物线过点(4,-8),所以16=-8m,即m=-2,抛物线的方程为x2=-2y.综上,抛物线的标准方程为y2=16x或x2=-2y.(3)由得由得所以所求抛物线的焦点坐标为(0,-2)或(4,0).当焦点为(0,-2)时,由=2,得p=4,所以所求抛物线方程为x2=-8y;当焦点为(4,0)时,由=4,得p=8,所以所求抛物线方程为y2=16x.综上所述,所求抛物线方程为x2=-8y或y2=16x.求抛物线的标准方程求抛物线方程都是先定位,即根据题中条件确定抛物线的焦点位置;后定量,即求出方程中的p值,从而求出方程.1.定义法:先判定所求点的轨迹是否符合抛物线的定义,进而求出方程.2.待定系数法:先设出抛物线的方程,再根据题中条件,确定参数值.(1)对于对称轴确定,开...