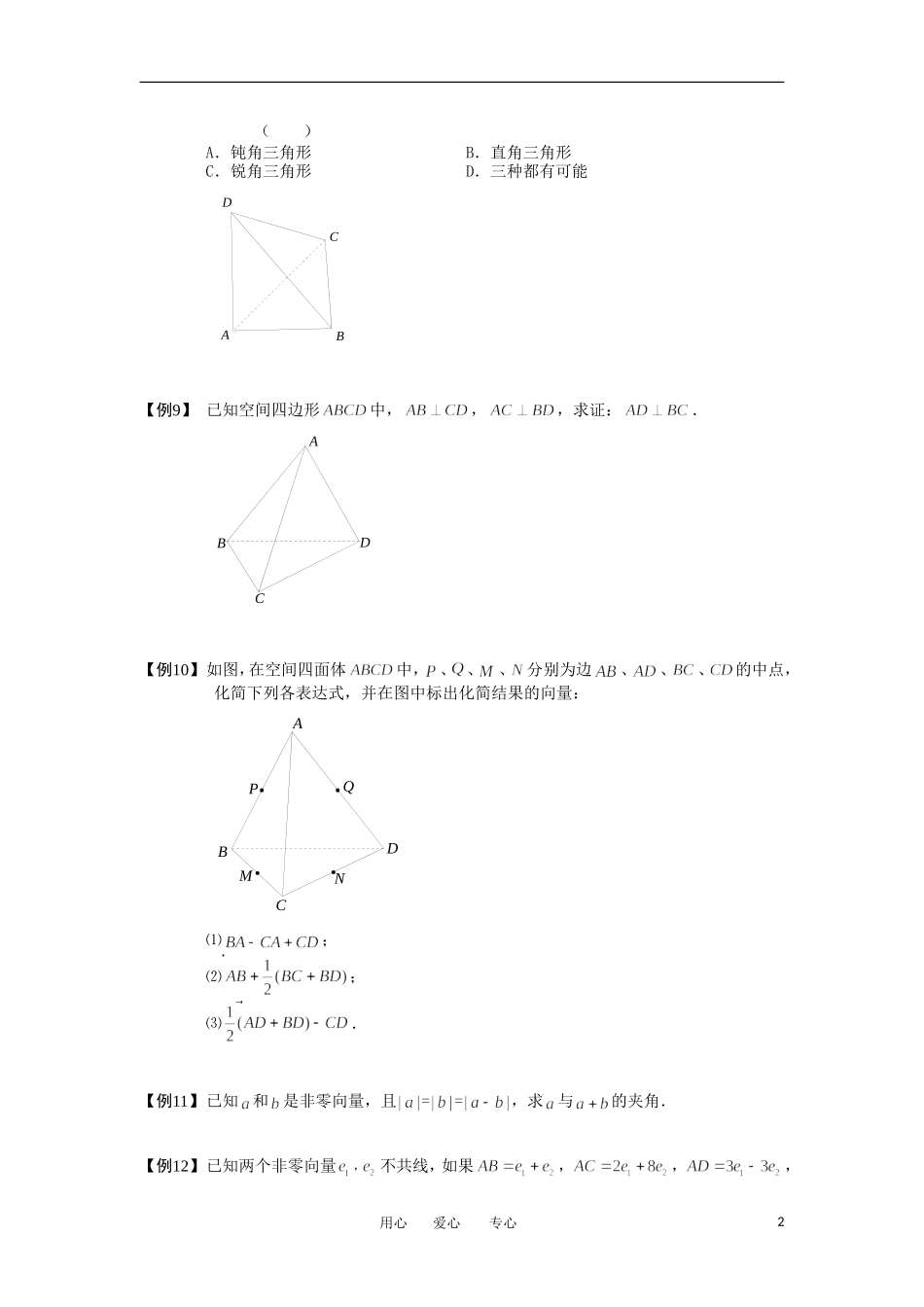
学而思高中完整讲义:空间向量与立体几何.板块五.用空间向量解柱体问题(2).学生版典例分析【例1】关于空间向量的四个命题中正确的是()A.若,则、、三点共线B.若,则、、、四点共面C.为直角三角形的充要条件是D.若为空间的一个基底,则构成空间的另一个基底【例2】在平行六面体中,下列四对向量:①与;②与;③与;④与.其中互为相反向量的有对,则()A.B.C.D.【例3】已知正方体中,,若,则,.【例4】空间四边形中,,点在上,且,为的中点,则_______.(用向量来表示.).【例5】棱长为的正四面体中,的值等于.【例6】已知空间四边形,点,分别为,的中点,且,,,用,,表示,则_______________.【例7】平行六面体中,为和的交点,设,化简:①;②;③;④.【例8】设是空间不共面的四点,且满足,则用心爱心专心1()A.钝角三角形B.直角三角形C.锐角三角形D.三种都有可能DCBA【例9】已知空间四边形中,,,求证:.DCBA【例10】如图,在空间四面体中,、、、分别为边、、、的中点,化简下列各表达式,并在图中标出化简结果的向量:DNMQPCBA⑴;⑵;⑶.【例11】已知和是非零向量,且==,求与的夹角.【例12】已知两个非零向量不共线,如果,,,用心爱心专心2求证:共面;【例13】已知三点不共线,对空间中一点,满足条件,试判断:点与是否一定共面?【例14】设四面体的对边,的中点分别为,;,的中点分别为,;,的中点分别为,时,试证明三线段,,的中点重合.UVSRQPBCAO【例15】已知斜三棱柱,设,在面对角线和棱上分别取点和,使得,求证:与向量共面.【例16】如图所示,在平行六面体中,是的中点,是的中点,是的中点,点在上,且,设,用基底表示以下向量:⑴;⑵;⑶;⑷.【例17】已知空间四边形,连结,设分别是的中点,化简下列各表达式,并标出化简结果向量:⑴;⑵;⑶.用心爱心专心3GMDCBA【例18】已知三棱锥,,,,,,、分别是棱、的中点,求:直线与所成角的余弦值.【例19】已知是边长为的正三角形所在平面外一点,且,,分别是,的中点,求异面直线与所成角的余弦值.【例20】已知平行六面体,如图,在面对角线,上分别取点,,使,,记,,,⑴若,用基底表示向量、、、.⑵求证:向量与向量,共面.NMD'C'B'A'DCBA【例21】已知三个非零向量不共面,,,,求证:这三个向量共面;【例22】设点为空间任意一点,点是空间不共线的三点,又点满足等式:,其中,求证:四点共面的充要条件是.【例23】如图,在空间四边形中,,,,,,,求与的夹角的余弦值.用心爱心专心4CBAO【例24】如图,已知矩形和矩形所在平面互相垂直,点分别是对角线的中点.求证:平面.NMFEDCBA【例25】已知三点不共线,对空间中一点,满足条件,试判断:点与是否一定共面?【例26】如图,已知空间四边形,其对角线,分别是对边的中点,点在线段上,且,用基底向量表示向量.GCBANMO【例27】如图,在四面体中,分别为边的中点,为的重心.⑴求证:.⑵记,,,用基底表示向量、、.用心爱心专心5DGNMQPCBA【例28】在的二面角的棱上,有两点,线段、分别在二面角的两个面内,且都垂直于,已知,,.⑴求的长度;⑵求与平面所成的角.EDCBA用心爱心专心6