高中数学 函数y＝Asin(ωx＋φ)图像(2课时)教案 北师大版 必修4VIP免费

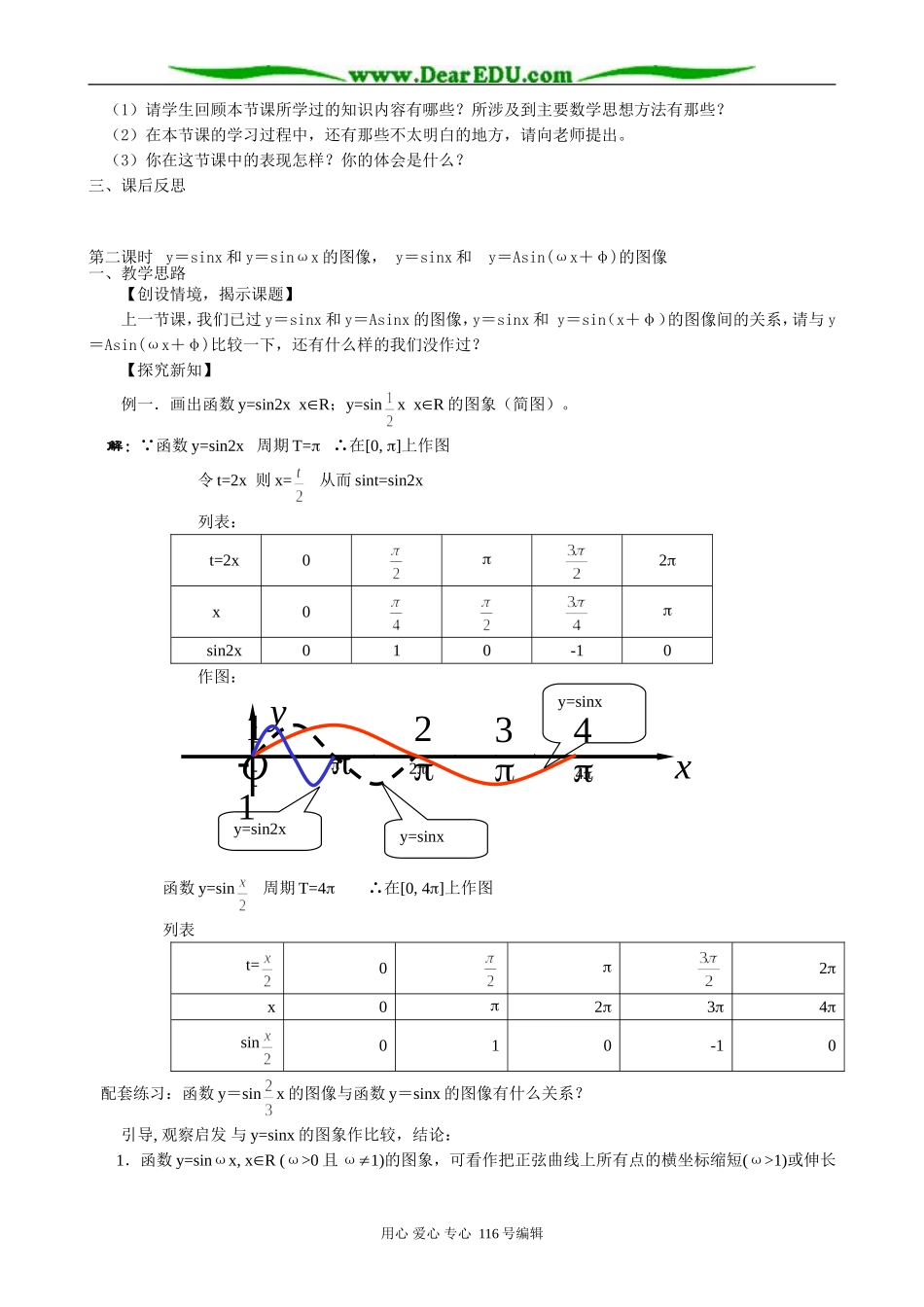
函数y＝Asin(ωx＋φ)的图象（2课时）一、教学目标：1、知识与技能（1）熟练掌握五点作图法的实质；（2）理解表达式y＝Asin(ωx＋φ)，掌握A、φ、ωx＋φ的含义；（3）理解振幅变换和周期变换的规律，会对函数y＝sinx进行振幅和周期的变换；（4）会利用平移、伸缩变换方法，作函数y＝Asin(ωx＋φ)的图像；（5）能利用相位变换画出函数的图像。2、过程与方法通过学生自己动手画图像，使他们知道列表、描点、连线是作图的基本要求；通过在同一个坐标平面内对比相关的几个函数图像，发现规律，总结提练，加以应用；要求学生能利用五点作图法，正确作出函数y＝Asin(ωx＋φ)的图像；讲解例题，总结方法，巩固练习。3、情感态度与价值观通过本节的学习，渗透数形结合的思想；树立运动变化观点，学会运用运动变化的观点认识事物；通过学生的亲身实践，引发学生学习兴趣；创设问题情景，激发学生分析、探求的学习态度；让学生感受图形的对称美、运动美，培养学生对美的追求。二、教学重、难点重点:相位变换的有关概念，五点法作函数y＝Asin(ωx＋φ)的图像难点:相位变换画函数图像，用图像变换的方法画y＝Asin(ωx＋φ)的图像三、学法与教学用具在前面，我们知道精确度要求不高时，可以用五点作图法，是哪五个关键点；首先请同学们回忆，然后通过物理学中的几个情境引入课题；主要让学生动手实践，两节课尽可能多地让他们画图，教师只是加以点拨；可以从几个具体的、简单的例子开始，在适当的时候加以推广；先分解各个小知识点，再综合在一起，上升更高一层。教学用具:投影机、三角板第一课时y＝sinx和y＝Asinx的图像，y＝sinx和y＝sin（x＋φ）的图像一、教学思路【创设情境，揭示课题】在物理和工程技术的许多问题中，经常会遇到形如y＝Asin(ωx＋φ)的函数，例如：在简谐振动中位移与时间表的函数关系就是形如y＝Asin(ωx＋φ)的函数。正因为此，我们要研究它的图像与性质，今天先来学习它的图像。【探究新知】例一．画出函数y=2sinxxR；y=sinxxR的图象（简图）。解：由于周期T=2∴不妨在[0,2]上作图，列表：作图：用心爱心专心116号编辑x02sinx010-102sinx020-20sinx00-0xyO2122112-2-12y=2sinxy=sinxy=sinx配套练习：函数y＝sinx的图像与函数y＝sinx的图像有什么关系？引导,观察,启发：与y=sinx的图象作比较，结论：1．y=Asinx，xR(A>0且A1)的图象可以看作把正数曲线上的所有点的纵坐标伸长(A>1)或缩短(00)个单位或向右平移－φ个单位(φ＜0＝得到的。性质讨论：不变的有定义域、值域、最值、周期变化的有奇偶性、单调区间与单调性由上例和练习可以看出：在函数y=sin（x＋φ），xR(φ0)中，φ决定了x＝0时的函数，通常称φ为初相，x＋φ为相位。【巩固深化，发展思维】课堂练习：P52练习第3题二、归纳整理，整体认识用心爱心专心116号编辑x+02xsin(x+)010-10xO134y=sin(x-)y=sin(x+)2y=sinx（1）请学生回顾本节课所学过的知识内容有哪些？所涉及到主要数学思想方法有那些？（2）在本节课的学习过程中，还有那些不太明白的地方，请向老师提出。（3）你在这节课中的表现怎样？你的体会是什么？三、课后反思第二课时y＝sinx和y＝sinωx的图像，y＝sinx和y＝Asin(ωx＋φ)的图像一、教学思路【创设情境，揭示课题】上一节课，我们已过y＝sinx和y＝Asinx的图像，y＝sinx和y＝sin（x＋φ）的图像间的关系，请与y＝Asin(ωx＋φ)比较一下，还有什...