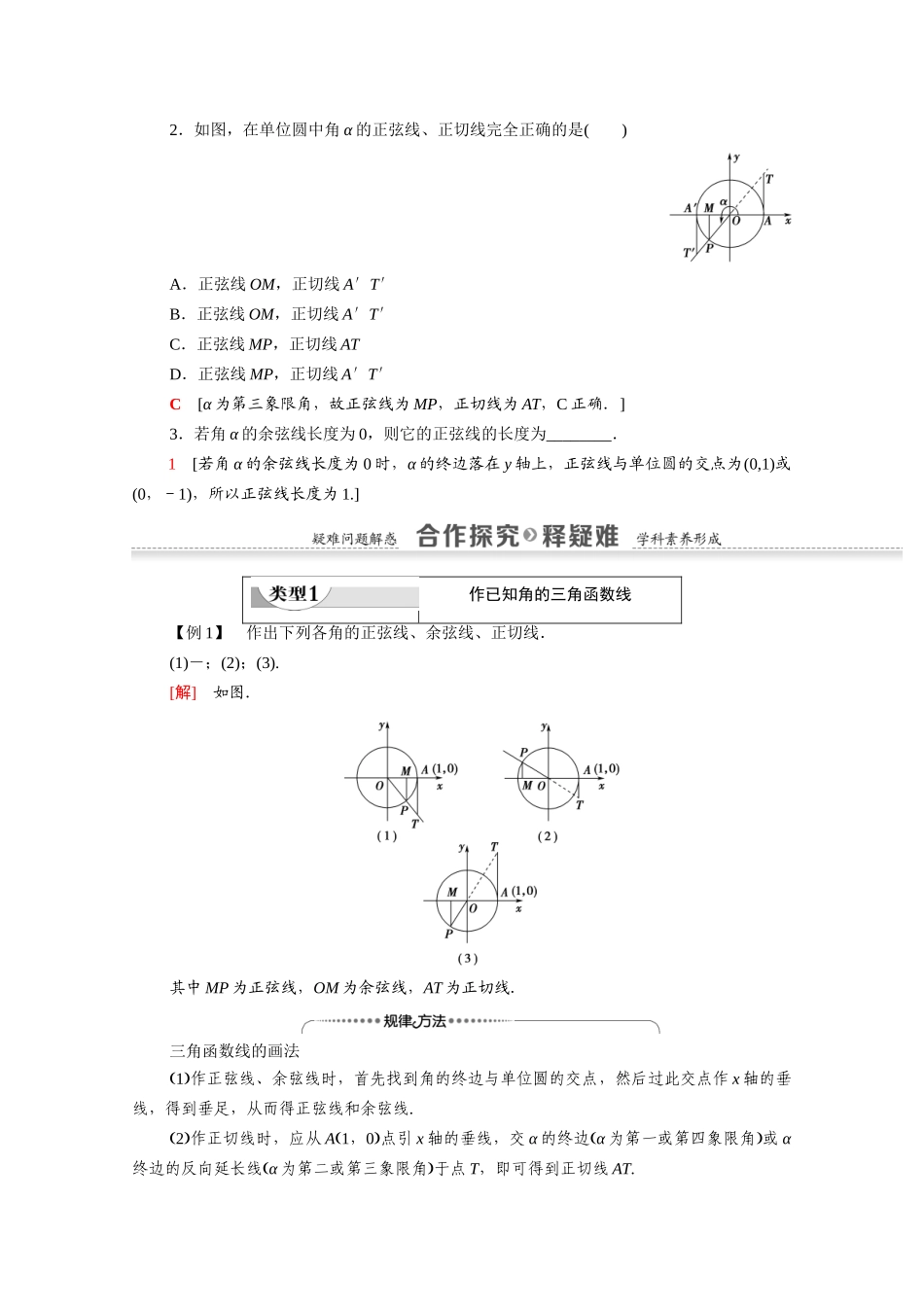
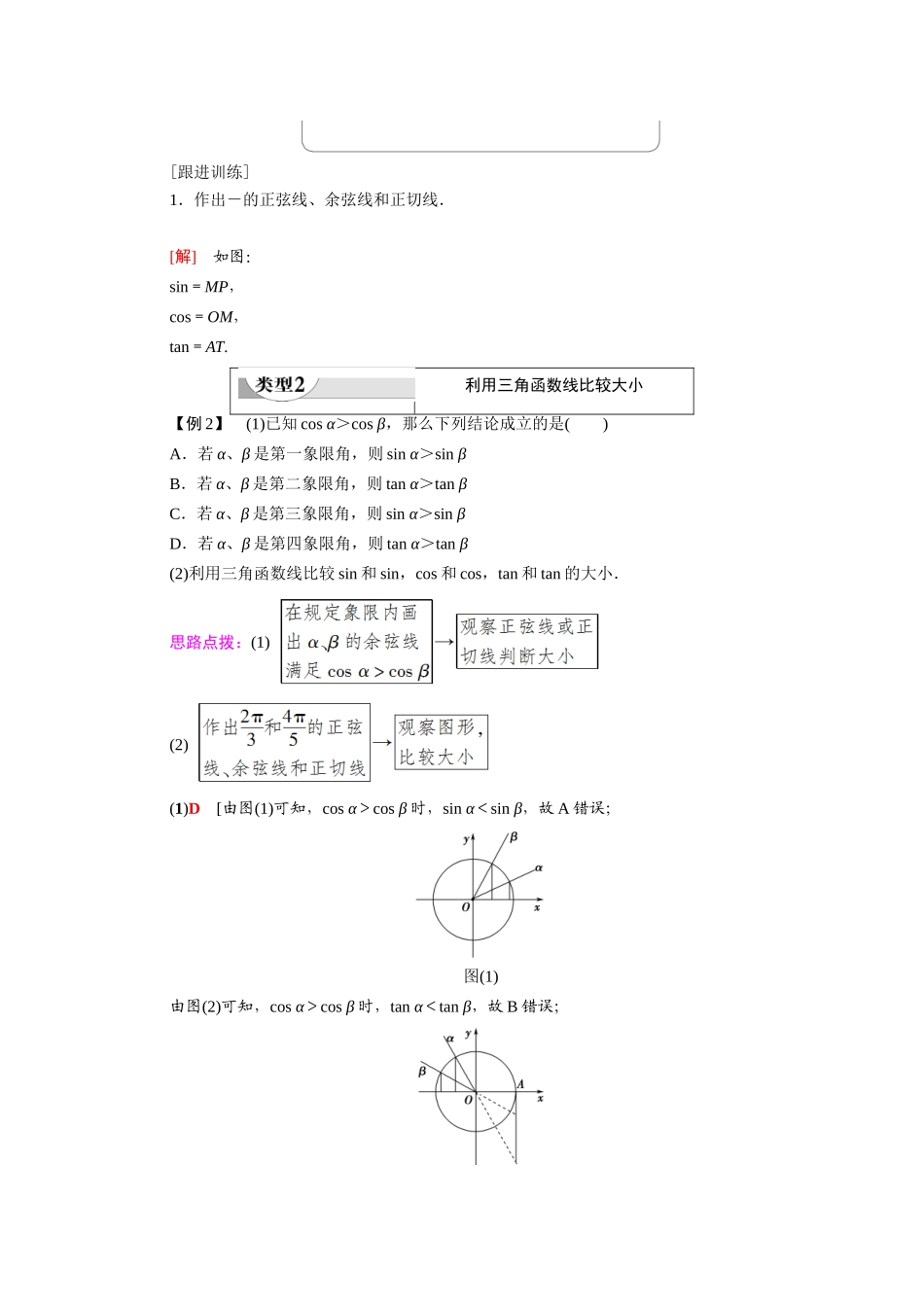
第2课时三角函数线及其应用学习目标核心素养1.了解三角函数线的意义,能用三角函数线表示一个角的正弦、余弦和正切.(重点)2.能利用三角函数线解决一些简单的三角函数问题.(难点)通过三角函数线的学习,培养学生数学抽象,直观想象和数学建模素养.1.有向线段(1)定义:带有方向的线段.(2)表示:用大写字母表示,如有向线段OM,MP.2.三角函数线(1)作图:①α的终边与单位圆交于P,过P作PM垂直于x轴,垂足为M.②过A(1,0)作x轴的垂线,交α的终边或其反向延长线于点T.(2)图示:(3)结论:有向线段MP、OM、AT,分别叫做角α的正弦线、余弦线、正切线,统称为三角函数线.思考:当角的终边落在坐标轴上时,正弦线、余弦线、正切线变得怎样?提示:当角的终边落在x轴上时,正弦线、正切线分别变成了一个点;终边落在y轴上时,余弦线变成了一个点,正切线不存在.1.角和角有相同的()A.正弦线B.余弦线C.正切线D.不能确定C[角和角的终边互为反向延长线,所以正切线相同.]2.如图,在单位圆中角α的正弦线、正切线完全正确的是()A.正弦线OM,正切线A′T′B.正弦线OM,正切线A′T′C.正弦线MP,正切线ATD.正弦线MP,正切线A′T′C[α为第三象限角,故正弦线为MP,正切线为AT,C正确.]3.若角α的余弦线长度为0,则它的正弦线的长度为________.1[若角α的余弦线长度为0时,α的终边落在y轴上,正弦线与单位圆的交点为(0,1)或(0,-1),所以正弦线长度为1.]作已知角的三角函数线【例1】作出下列各角的正弦线、余弦线、正切线.(1)-;(2);(3).[解]如图.其中MP为正弦线,OM为余弦线,AT为正切线.三角函数线的画法1作正弦线、余弦线时,首先找到角的终边与单位圆的交点,然后过此交点作x轴的垂线,得到垂足,从而得正弦线和余弦线.2作正切线时,应从A1,0点引x轴的垂线,交α的终边α为第一或第四象限角或α终边的反向延长线α为第二或第三象限角于点T,即可得到正切线AT.[跟进训练]1.作出-的正弦线、余弦线和正切线.[解]如图:sin=MP,cos=OM,tan=AT.利用三角函数线比较大小【例2】(1)已知cosα>cosβ,那么下列结论成立的是()A.若α、β是第一象限角,则sinα>sinβB.若α、β是第二象限角,则tanα>tanβC.若α、β是第三象限角,则sinα>sinβD.若α、β是第四象限角,则tanα>tanβ(2)利用三角函数线比较sin和sin,cos和cos,tan和tan的大小.思路点拨:(1)(2)(1)D[由图(1)可知,cosα>cosβ时,sinα<sinβ,故A错误;图(1)由图(2)可知,cosα>cosβ时,tanα<tanβ,故B错误;图(2)由图(3)可知,cosα>cosβ时,sinα<sinβ,C错误;图(3)由图(4)可知,cosα>cosβ时,tanα>tanβ,D正确.]图(4)(2)解:如图,sin=MP,cos=OM,tan=AT,sin=M′P′,cos=OM′,tan=AT′.显然|MP|>|M′P′|,符号皆正,∴sin>sin;|OM|<|OM′|,符号皆负,∴cos>cos;|AT|>|AT′|,符号皆负,∴tan<tan.1利用三角函数线比较大小的步骤:①角的位置要“对号入座”;②比较三角函数线的长度;③确定有向线段的正负.2利用三角函数线比较函数值大小的关键及注意点:①关键:在单位圆中作出所要比较的角的三角函数线.,②注意点:比较大小,既要注意三角函数线的长短,又要注意方向.[跟进训练]2.已知a=sin,b=cos,c=tan,则()A.a<b<cB.a<c<bC.b<c<aD.b<a<cD[由如图的三角函数线知:MP<AT,因为>=,所以MP>OM,所以cos<sin<tan,所以b<a<c.]3.设<α<,试比较角α的正弦线、余弦线和正切线的长度.如果<α<,上述长度关系又如何?[解]如图所示,当<α<时,角α的正弦线为MP,余弦线为OM,正切线为AT,显然在长度上,AT>MP>OM;当<α<时,角α的正弦线为M′P′,余弦线为OM′,正切线为AT′,显然在长度上,AT′>M′P′>OM′.利用三角函数线解三角不等式[探究问题]1.利用三角函数线如何解答形如sinα≥a,sinα≤a(|a|≤1)的不等式?提示:对形如sinα≥a,sinα≤a(|a|≤1)的不等式:图①画出如图①所示的单位圆;在y轴上截取OM=a,过点(0,a)作y轴的垂线交单位圆于两点P和P′,并作射线...